Abstract
Elastography is emerging as an imaging modality that can distinguish normal versus diseased tissues via their biomechanical properties. This article reviews current approaches to elastography in three areas — quasi-static, harmonic, and transient — and describes inversion schemes for each elastographic imaging approach. Approaches include: first-order approximation methods; direct and iterative inversion schemes for linear elastic; isotropic materials; and advanced reconstruction methods for recovering parameters that characterize complex mechanical behavior. The paper’s objective is to document efforts to develop elastography within the framework of solving an inverse problem, so that elastography may provide reliable estimates of shear modulus and other mechanical parameters. We discuss issues that must be addressed if model-based elastography is to become the prevailing approach to quasi-static, harmonic, and transient elastography: (1) developing practical techniques to transform the ill-posed problem with a well-posed one; (2) devising better forward models to capture the transient behavior of soft tissue; and (3) developing better test procedures to evaluate the performance of modulus elastograms.
1. Introduction
Elastography is an emerging imaging modality that exploits differences in the biomechanical properties of normal and diseased tissues (Krouskop et al., 1998; Samani et al., 2007; Sarvazyan et al., 1995; Parker et al., 2011). Several groups have investigated the diagnostic value of elastography in various clinical settings; these include detecting and characterizing atherosclerotic plaques (de Korte et al., 2002; de Korte et al., 2000; Doyley et al., 2001; Brusseau et al., 2001; Woodrum et al., 2006); guiding minimally invasive therapeutic techniques (Kallel et al., 1999; Righetti et al., 1999; Varghese et al., 2003); and improving the differential diagnosis of breast and prostate cancers (Hiltawsky et al., 2001).
Elastography was developed in the late 1980s to early 1990s to improve the diagnostic value of ultrasonic imaging (Lerner and Parker, 1987; Lerner et al., 1988; O’Donnell et al., 1994; Ophir et al., 1991), but the success of ultrasonic elastography has inspired other investigators to develop analogues based on other imaging modalities; these include magnetic resonance elastography (Muthupillai et al., 1995; Bishop et al., 2000; Weaver et al., 2001; Sinkus et al., 2000), and optical coherence tomography elastography (Khalil et al., 2005; Kirkpatrick et al., 2006; Ko et al., 2006).
Although current approaches to elastography vary considerably, we can summarize the general principles of elastography as follows: (1) perturb the tissue using a quasi-static, harmonic, or transient mechanical source; (2) measure the internal tissue displacements using a suitable ultrasound, magnetic resonance, or optical displacement estimation method; and (3) infer the mechanical properties from the measured mechanical response, using either a simplified or continuum mechanical model. Several review articles provide a comprehensive overview of different approaches to elastography (Bamber et al., 2002; Greenleaf et al., 2003; Manduca et al., 1998; Ophir et al., 2000; Parker et al., 2011). This article provides a brief description of current approaches. To simplify our discussion, we classify current approaches to elastography into three groups: quasi-static, harmonic, and transient; and review a selection of inverse reconstruction schemes (methods for reconstructing shear modulus, viscosity, nonlinearity, and anisotropy within soft tissues) that have been proposed for each elastographic-imaging approach. The primary goal of this review is to document the efforts made by several groups, including that of the author, to develop elastography within the framework of solving an inverse problem (i.e., model-based elastography), a strategy that is beginning to transform elastography from an imaging modality that provides only an approximate estimate of shear modulus to one that can provide reliable estimates of shear modulus and other mechanical parameters — namely viscosity, anisotropy, poro-elasticity, and nonlinearity.
This paper surveys elastographic approaches from the simplest to the most complex and computationally intensive, and is organized into six sections. Section 2 examines the basic first-order approximation methods employed in earlier work. Section 3 covers the direct (or forward) problem in elasticity imaging. Section 4 then considers the major categories of inversion schemes under linear elastic, isotropic models. Section 5 reviews approaches to more complex models including viscoelastic, poroelastic, nonlinear, and anisotropic behaviors. Finally, section 6 describes issues that still remain to be addressed.
2. First order approximation to shear modulus
Several groups have developed approaches for obtaining approximate estimates of shear modulus, and despite their limited accuracy these techniques are fast and robust — traits that make them clinically appealing. In this section, we review the methods that have been proposed for obtaining approximate estimates of shear modulus in quasi-static, harmonic, and transient elastography. Figure 1 provides a pictorial representation of all three approaches to elastography.
Figure 1.
Schematic representation of current approaches to elastographic imaging: quasi-static elastography (left), harmonic elastography (middle), and transient elastography (right).
2.1 Quasi-static elastography based on stress uniformity
Ophir et al. (1991) proposed a quasi-static method that is arguably the most established approach to elastography. Quasi-static elastography was originally developed as an ultrasound imaging technique (O’Donnell et al., 1994; Ophir et al., 1991; Bamber and Bush, 1995), but a magnetic resonance (MR) analogue was later described (Plewes et al., 2000; Fowlkes et al., 1995). Quasi-static elastography measures the axial strain induced within the tissue using either an external or internal source. A small motion is induced within the tissue (typically on the order of 2 % of the axial dimension) with a quasi-static mechanical source; the axial component of the internal tissue displacement is then measured, usually by performing cross-correlation analysis on pre- and post-deformed radio-frequency (RF) echo frames in the time or frequency domain; and strain elastograms are produced by spatially differentiating the axial component of displacement, using either a finite difference or a least squares strain estimator (Kallel and Ophir, 1997). In quasi-static elastography, soft tissues are typically envisioned as a series of one-dimensional springs that are arranged in a simple fashion. For this simple mechanical model, the measured strain (ε ) is related to the internal stress (σ ) as follows (Hooke’s Law):
| (1) |
where E is the Young’s modulus of the tissue. Currently, no method can measure the internal stress distribution in vivo; consequently, in quasi-static elastography, the internal stress distribution is typically assumed to be constant (i.e., σ ≈ 1). Using this assumption, an approximate estimate of Young’s modulus is computed from the reciprocal of the measured strain, but the disadvantage of computing modulus elastograms in this manner is that stress concentration and target hardening artifacts (Konofagou et al., 1996; Ponnekanti et al., 1994) may compromise the diagnostic quality of the ensuing images. In spite of this limitation, Kallel et al. (1998) demonstrated that this approach can provide a good relative estimate of the shear modulus of low-contrast focal lesions, in cases for which uniform stress is induced within the imaging field of view. Several groups have adopted this approach to obtain reasonable relative estimates of shear modulus for which accurate quantification of shear modulus is not essential; these include guiding minimally invasive therapeutic techniques, and detecting abnormalities in several organs such as the breast, prostate, and liver tissue. Figure 2 shows an example of an approximate modulus elastogram computed using the assumption of stress uniformity; the strain images were filtered using the spatial filter described in (Doyley et al., 2005) prior to inversion.
Figure 2.

Modulus elastogram obtained from a phantom containing a single 10 mm diameter inclusion whose modulus contrast was approximately 6.03 dB. The modulus elastogram was derived by taking the reciprocal off the strain elastogram after spatial filtering.
2.2 Harmonic elastography base ed on local frequency estimation
Like its quasi-static counterpart t, harmonic elastography was first proposed as an ultrasound imaging method (Lerner and Parker, 1987; Lerner et al., 1988; Parker et al., 1990; Yamakoshi et al., 1990), but was later extended to magnetic c resonance imaging (MRI) (Muthupillai et al., 1995), and is now the prevailing approach to magnettic resonance elastography (MRE). In harmonic elastography, a low-frequency acoustic wave (typiccally < 1 kHz) is transmitted within the tisssue using a sinusoidal mechanical source. The phase and a amplitude of the propagating waves are visuualized using either color Doppler imaging (Parker et al., 1990; Lerner et al., 1990; Yamakoshi et al., 1990) or phase-contrast MR imaging (Muthupillai et al., 1995; Sinkus et al., 2000; Weaver et al., 2001). Assuming that shear waves propagate with plane wavefronts, then an approximate estimate of the local shear modulus (μ ) may be computed from local estimates of o the wavelength as follows:
| (2) |
where c2 is the velocity of the shear wave, and ρ is the density of the tissue. Manduca et al. (2001) showed that in a homogeneous tissue, shear modulus can be estimated from local estimates of instantaneous frequency, which they computed with a bank of wavelet filters as described in (Knutsson et al., 1994). Wu et al. (2006) used a similar approach to compute shear modulus images with sonoelastography (i.e., the ultrasound analogue to MRE). Although this shear-modulus estimation approach is relatively insensitive to measurement noise, the spatial resolution of the ensuing modulus elastograms is limited. A further weakness of the approach is that the plane-wave approximation breaks down in complex organs, such as the breast and brain, when waves reflected from internal tissue boundaries interfere constructively and destructively.
2.3 Transient elastography based on arrival time estimation
A major limitation of harmonic elastography is that shear waves attenuate rapidly as they propagate within soft tissues, which limits the depth of penetration. To overcome this limitation, Sarvazyan et al. (1998) proposed a transient approach to elastography that uses the acoustic radiation force (ARF) of an ultrasound transducer to perturb tissue locally. Nightingale et al. (2003) were the first to implement this technique on a clinical ultrasound scanner to assess the viscoelastic properties of the liver. A MR analog has been reported in (McCracken et al., 2004; Souchon et al., 2008). Bercoff et al. (2004) also developed a transient approach to elastography that they call supersonic shear-wave imaging (SSI), which is rapidly becoming the most established approach to ultrasonic elastography. This elastographic imaging method uses an ultrasound scanner with an ultra-high frame rate (i.e., 10,000 fps) to track the propagation of shear waves. As in harmonic elastography, local estimates of shear modulus are estimated from local estimates of wavelength via equation (2) in transient elastography. However, the reflections of shear waves at internal tissue boundaries make it difficult to measure shear-wave velocity. Ji et al. (2003) proposed to overcome this limitation by computing wave speeds directly from the arrival times.
McAleavey et al. (2009) proposed to measure the shear modulus distribution within soft tissues using a technique known as spatially modulated ultrasound radiation force (SMURF) imaging. This elastographic imaging technique uses radiation force to generate a shear wave of known spatial frequency, and then measures the temporal frequency response of the vibrating tissue as the wave propagates past a point.
Fatemi and Greenleaf (1998) proposed a technique known as vibroacoustography that uses radiation force to vibrate tissues in the kHZ range, by using two overlapping ultrasound beams with slightly different frequencies. The resulting tissue mechanical response is dependent on the local acoustic mechanical properties of tissue that are obtained using a hydrophone. Using this technique, Fatemi and Greenleaf demonstrated that vibroacoustography could visualize microcalcification with high contrast resolution.
3. Solving the direct elasticity problem
To solve the inverse elasticity problem, we need an accurate model to predict the strains and/or displacements incurred when a tissue of known biomechanical properties and boundary conditions is perturbed using a pseudo-static, harmonic or transient mechanical source (i.e., solving the direct problem). Solving the direct problem provides the computational basis for solving the inverse problem: estimating the mechanical properties (i.e., the unknowns) from the measured mechanical responses. The advantage of this approach to elastography is that both the direct and inverse problems are formulated from well-established physical laws, which provide equations that relate the biomechanical properties (namely shear modulus, Poisson’s ratio, anisotropy, viscosity, non-linearity, and poroelasticity) to the measured mechanical response.
3.1 Equations of motion
We can derive a system of partial differential equations (PDEs) from the conservation of linear momentum to describe the direct elasticity problem. These equations are given in compact form by (Timoshenko and Goodier, 1970; Fung, 1981):
| (3) |
where σij is the three-dimensional stress tensor (i.e., a vector of vectors), fi is the deforming force, and ▽ is the del operator. Assuming that soft tissues exhibit linear elastic behavior, which is valid for infinitesimal deformations, then we can relate the strain tensor (εkl ) to the stress tensor (σij) as follows (Landau et al., 1986):
| (4) |
where the tensor C is the Christoffel rank-four tensor consisting of 21 independent elastic constants (Greenleaf et al., 2003; Ophir et al., 1999; Fung, 1981). Developing methods to estimate all 21 elastic parameters is not trivial; therefore, several assumptions are used to reduce the number of independent elastic constants. The most common assumption, and perhaps the simplest, is that soft tissues exhibit linear, purely elastic isotropic mechanical behavior (i.e., that soft tissues behave like Hookian material). In this case, only two independent constants, λ ( the second Lamé constant) and μ (shear modulus), are required to describe the mechanical behavior of soft tissues. However, this assumption is clearly not true for some tissues, as discussed in Section 5. The constitutive relation that describes the relationship between stress and strain for linear isotropic elastic materials is given by:
| (5) |
where δij is the Kronecker delta, Δ = △ ·u = ε11 +ε22 +ε33 is the compressibility relation, and the components of the strain tensor are defined as:
| (6) |
where and uj are the displacement components in the Cartesian coordinates xi Lamé constants (i.e., λ and μ ) are related to traditional engineering constants, such as Young’s modulus (E) and Poisson’s ratio (v), as follows (Timoshenko and Goodier, 1970; Fung, 1981):
| (7) |
Since stress cannot be measured in vivo, it is typically eliminated from the equilibrium equations (i.e., equation (3)) using equation (5), and the strain components can be expressed in terms of displacements, using equation (6). The resulting equations of equilibrium (i.e., the Navier-Stokes equations) are given by:
| (8) |
where ρ is density is the density of the material, and t is time. For quasi-static deformations, equation (8) reduces to:
| (9) |
For harmonic deformations, the displacement field is assumed to have a time harmonic form that is given by (Sinkus et al., 2000; Van Houten et al., 2001):
| (10) |
where 𝕽is the real component of the time harmonic displacement. The time-independent (steady-state) equations in the frequency domain give:
| (11) |
where ω is the angular frequency of the sinusoidal excitation. For transient deformations, the wave equation is derived by differentiating equation (8) with respect to x,y,z, which gives the following result (Timoshenko and Goodier, 1970):
| (12) |
where the velocity of the propagating compressional wave, C1, is given by:
| (13) |
To derive the wave equation for the propagating shear wave, an operation of curl is peformed on equation (8), which gives:
| (14) |
where ζ = △ × u /2 is the rotational vector, and the shear-wave velocity, c2, is given by:
| (15) |
3.2 Numerical solution of governing equations
The equations that describe the direct problem for quasi-static, harmonic and transient elastographic imaging methods have been solved using analytical methods (Bilgen and Insana, 1998; Kallel et al., 1996; Love, 1929; Sumi et al., 1995a) for simple geometries and boundary conditions. However, it is more useful to solve these equations on irregular domains for elastically heterogeneous tissue, which is difficult to perform using analytical methods. Consequently, investigators have employed numerical methods — namely, the finite-element method (McLaughlin and Renzi, 2006; Parker et al., 1990; Ponnekanti et al., 1994; Van Houten et al., 2001; Samani et al., 2001; Miga, 2003; Konofagou et al., 1996; Hall et al., 1997; Brigham et al., 2007), and the finite-difference method (Raghavan and Yagle, 1994; Sinkus et al., 2000; O’Donnell et al., 1994) — to solve the governing equations for all three approaches to elastography. However, the finite element method (FEM) is currently the most popular approach for solving PDEs, which is not surprising because: (1) it analyzes structures with complex geometries and boundary conditions more easily than other numerical methods; and (2) several powerful FEM packages are commercially available (such as ANSYS, MARC, COMSOL, Abaqcus, and NASTRAN).
A finite-element representation of the governing PDEs involves four steps. First, the geometry of the tissue is segmented into a series of finite elements, through a process known as mesh generation. The design of efficient, two- and three-dimensional mesh generators is an area of active research (Geuzaine and Remacle, 2009; Pinheiro et al., 2008; Triantafyllidis and Labridis, 2002). However, the main requirement for an efficient mesh generator is that it should be capable of meshing an object that is composed of both smooth and irregular surfaces (Lionheart, 2004). Second, a weak form of the governing PDEs is derived, using either the variational or the weighted residual method (Reddy, 1993; Cook et al., 1989). Third, a basis or shape function is substituted in the derived equation to produce a system of linear algebraic equations, which has the following form:
| (16) |
where the matrix [K] is the global stiffness or coefficient matrix, f is the global force vector, and u is the vector of unknown displacements. The final step involves imposing the external boundary conditions associated with equation (16) before solving the resulting equations.
3.2.1 Weak form
The weak form is a weighted-integral statement that is equivalent to the governing partial differential equation and the natural boundary conditions of the problem. The weak form of the governing elasticity equation for each approach to elastographic imaging can be derived as described in (Reddy, 1993). For simplicity, we will describe only the finite element implementation for the harmonic case (i.e., equation (8)), since the procedure is identical for the quasi-static and transient cases. The weak form of equation (8) with a scalar weighting function ϕi(x, y, z) is given by:
| (17) |
where represents an integration over the boundary ( Γ) of the element, ϕi is a scalar basis associated Γ with the element, n̂ represents the outward-pointing normal vector, and t̂ represents the Nuemann boundary condition. If the scalar components of the displacement vector, u, are u(x, y, z),v,(x, y, z),w(x, y, z) in the x,y, and z directions, respectively, then the Galerkin approximation of the displacement may be derived by expanding the scalar components in the ϕ basis to give:
| (18) |
where N is the number of nodes associated with each element in the finite element mesh and uj ,vj , wj are the axial, lateral, and elevational displacement components at each element node. The Galerkin weak-form finite element model is obtained by substituting equation (18) into equation (17):
| (19) |
where f is the 3N × 1 global force vector and K(μ,λ,ρ ) that is given by
| (20) |
where the coefficients of the global stiffness matrix are determined by the basis function and the material properties (i.e., μ and λ ).
3.2.2 Dimensionality reduction using the plane-strain and plane-stress approximation
Despite the technological advances in 3D ultrasound imaging, ultrasound is predominately a two-dimensional imaging modality. Thus, most investigators in ultrasonic imaging typically reduce the 3D elasticity problem to a two-dimensional problem, using either a plane-strain or plane-stress approximation. To illustrate the differences between the two approximations, let’s consider a linear elastic 1 1 solid, Ω, of uniform thickness, h , bounded by two parallel planes ( and ) and a closed 2 2 boundary, Γ. If the thickness of h≫Ω, then the problem can be considered a plane-strain problem. In this case, we assume thatε13 = ε23 = ε33 = 0. The plane-strain approximation is typically used when structures above and below the ultrasound scan plane have motion confined to the elevation (z) direction (Kallel et al., 2001; Doyley et al., 2000; Skovoroda et al., 1995; Barbone and Bamber, 2002). However, when h≪Ω, the problem is considered a plane-stress problem. In this case, we assume that σ13 = σ23 = σ33 = 0). The plane-stress approximation generally applies to thin plates; however, (Sumi et al., 1995b) used a plane-stress approximation to reduce the 3D elasticity problem to 2D. In reality, the plane-strain and plane-stress assumptions are valid only for special cases such as phantoms with cylindrical inclusions, or when elastography is performed using the constrained imaging method described in (Kallel and Ophir, 1997). Therefore, errors are typically incurred when the 3D elasticity problem is modeled using either approximation.
4. Computing shear modulus by solving the inverse elasticity problem
Several groups have proposed inversion schemes for computing the mechanical properties within soft tissues. Figure 3 summarizes the inversion schemes proposed for the three different approaches to elastography. These inversion schemes were formulated based on the premise that soft tissue behaves like an Hookian material (i.e., it behaves like a linear, purely isotropic material).
Figure 3.
Hierarchical diagram of proposed approaches to shear modulus estimation for harmonic, transient, and quasi-static elastography, assuming linear elastic isotropic mechanical behavior.
4.1 Quasi-static elastographic inversion schemes
4.1.1 Direct inversion
Raghavan and Yagle (1994) proposed a direct inversion scheme for recovering shear modulus. They derived a linear system of equations by re-arranging the PDEs that describe the direct problem for the plane-strain condition. The PDEs that (Raghavan and Yagle, 1994) derived are given by:
| (21) |
where , the unknowns are shear modulus (μ ) and hydrostatic pressure ( p)1, and the coefficients are functions of the internal tissue strains that are related to the measured displacements (see equation (6)). The weakness of this approach is that both the shear modulus (μ ) and the hydrostatic pressure ( p ) on the boundary must be known to solve equation (21).
Although Rhagavan and Yagle’s computer simulation demonstrated that this inversion scheme could produce very encouraging displacements, they observed that the performance of the reconstructed elastograms degraded rapidly with increasing measurement noise. Another weakness of this inversion scheme is that no imaging system to date can measure hydrostatic pressure. To overcome this limitation, (Skovoroda et al., 1995) used an analytical method to eliminate the pressure term from equation (21). Eliminating the pressure term gives:
| (22) |
As in equation (21), the shear modulus must be known on the boundary of the region of interest (ROI) to solve equation (22). Skovoroda et al. (Skovoroda et al., 1995) were the first to demonstrate that this information could be obtained by exploiting the stress-continuity properties of soft tissues. They demonstrated that contours of small shear modulus variations could easily be defined, and that the modulus along the boundary could be computed by processing axial strain elastograms as follows:
| (23) |
where μr is the relative shear modulus, and and are the axial strains within and outside the boundary of ROI. Equation (22) contains high-order derivatives that will amplify measurement noise, which could compromise the quality of ensuing modulus elastograms as demonstrated in figure 4. Despite this potential limitation,, the viability of this inversion scheme has been demonstrated in gelatin and ex vivo kidney phantoms (Skovoroda et al., 1999; Skovoroda and Aglyamovv, 1995; Chenevert et al., 1998). Skovoroda et al. (1999) cast the inverse problem as an integral rather than a differential form — an approach that was first described in (Sumi et al., 1995b) — to make the technique less susceptible to measurement noise. To bolster performance further, they computed lateral displacement using the incompressible method described in (Lubinski et al., 1996).
Figure 4.
Modulus elastograms computed from (a) ideal axial and lateral strain estimates and (b) strain estimates that were corrupted with 4 % additive white noise. The simulated phantom m contained an inclusion with a Gaussian modulus distribution that had a peak contrast of 4:1. Courtesy off Dr. P. Barbone, Boston University Department of Mechanical and Aeronautical Engineering.
Bishop et al. (2000) proposed to eliminate the pressure term appearing in equation (21) by partitioning the matrix, rather than by doing this analytically as described in (Skovoroda et al., 1995). But the resulting formulation proved to be ill-conditioned. Consequently, (Bishop et al. a , 2000) constrained the solution by employing the Tikhonov regularization method.
Sumi et al. (1995b) also proposed a direct inversion scheme; however, they solved the inverse problem for the plane-stress case, using the following PDEs:
| (24) |
where the unknowns are spatial derivatives of relative Young’s modulus, and the coefficients are strains and their spatial derivatives. They computed the shear modulus at a given point (x, y) within the tissue relative to a reference point —let’s say: (A, B) — by employing a line integral. The feasibility of this inversion scheme has been demonstrated in phantoms and excised tissues (Sumi, 2007; Sumi and Nakayama, 1998); nevertheless, the plane-stress condition is typically not relevant for most clinical applications. To make the technique more clinically relevant, (Le Floc’h et al., 2009) extended the concept to the plane-strain case. The equations they derived for solving the inverse problem for the plane-strain condition are given in compact form as follows:
| (25) |
Although theoretically feasible, equation (28) is difficult to solve, because cannot be measured in practice. However, (Le Floc’h et al., 2009) demonstrated that the second term could be used to highlight the boundaries of different tissue types.
4.1.2 Iterative Inversion
The inverse problem can also be viewed as a parameter-optimization problem, where the goal is to find the shear modulus that minimizes the error between measured displacement or strain fields, and those computed by solving the direct problem. This inversion approach has been successfully used in several emerging medical imaging modalities, as discussed in (Paulsen et al., 2005; Yorkey et al., 1987), and was applied to elastography by (Kallel and Bertrand, 1996; Doyley et al., 1996). The objective function that is minimized typically has the following form:
| (26) |
where u is the solution to the direct problem computed from the shear modulus distribution, μ , by solving equation (9). Minimizing equation (29) with respect to shear modulus variations is a nonlinear process; however, we can do this iteratively using a variety of techniques as discussed in (Vogel, 2002). Proposed optimization techniques can be classified into three broad categories: (1) those that require only the value of the functional π for different values of the parameters μ (i.e., non-gradient approaches); (2) those that require the value of the functional and its derivative with respect to the material parameters (called the gradient vector); and (3) those that require the first and second derivative of the functional with respect to the material parameters (called the Hessian matrix). All three optimization methods are illustrated below.
(a) Hessian-based optimization method
The Gauss-Newton method is perhaps one of the most established optimization methods. Minimizing equation (26) using the Gauss-Newton method produces a matrix solution at the (i+1) iteration that has the general form:
| (27) |
where T denotes the transpose; I denotes an Identity matrix; Δμi is a vector of shear modulus updates at all coordinates in the reconstruction field; and J(μ i ) is the Jacobian, or sensitivity, matrix. The Hessian matrix, [J(μ i )T J(μ i )], is usually ill conditioned; therefore, to stabilize performance in the presence of measurement noise, the matrix is regularized using one of three variational methods: the Tikhonov (Kallel and Bertrand, 1996), the Marquardt (Doyley et al., 2000), or the total variational method (Richards et al., 2009; Jiang et al., 2009).
Moulton et al. (1995) computed the JacobIan matrix [J ] column-wise, where each column represents the difference between displacement computed when the direct problem was solved, once for a given shear modulus distribution and then again when the shear modulus of a single node, or element, was perturbed by unity. However, computing the Jacobian matrix in this fashion is very demanding. Kallel and Bertrand (1996) proposed a more efficient approach, which involved computing the derivative of the forward problem with respect to shear modulus at a given node — let’s say j — as follows:
| (28) |
The global stiffness matrix on the left-hand side of equation (28) requires factorization, and is the same matrix used to solve the direct problem at the previous iteration. Therefore, all that is required to compute each is a simple matrix back-substitution.
Solving the inverse problem using displacement boundary conditions (DBC) will provide only relative estimates of shear modulus. Doyley et al. (2000) demonstrated that to recover absolute values the pressure on the boundary must be known.
Rather than developing a custom optimization code, an increasing number of investigators have demonstrated that clinically useful elastograms can be computed using the FMINCON algorithm, which is part of MATLAB optimization toolbox (Jiang et al., 2009; Baldewsing et al., 2005a; Le Floc’h et al., 2009). The advantage of using FMINCON is that it doesn’t require the global stiffness matrix and force vector, and thus, allows the implementation of the inverse problem based on commercially available finite-element codes. Jiang et al. (2009) developed an edge-preserving, iterative, inverse-reconstruction approach based on FMINCON. They used this algorithm to demonstrate the feasibility of using model-based elastography to guide and monitor radio-frequency (RF) ablation. Figure 5 shows an example of modulus elastograms computed using this reconstruction approach.
Figure 5.
Sonogram (a), strain elastogram (b), and modulus elastogram (c) of RF ex vivo ablated bovine liver. Courtesy of Drs. T. J. Hall H , T. Varghese, and J. Jiang (University of Wisconsin -Madison).
The boundary between the ablated and normal tissue was better delinated in the modulus elastograms than the strain elastograms, which provided a better estimate of the extent of the thermal zone.
Miga et al. (2003) proposed a novel approach to elastography that they refer to as modality independent elastography (MIEE) which is based on a combination of the finite element method, the Gauss-Newton iterative scheme, and image similarity. In this technique the objective function that is minimized has the following form:
| (29) |
where STRUEis similarity values computed when the target image is compared to itself, S(E)EST is the similarity between the target and model-deformed source image using the current estimate of Young’s. Minimizing equation (29) with the Gauss Newton iteration scheme gives the following property updates:
| (30) |
where the Jacobian matrix.
Ou et al. (2008) demonstrated that 3D MIE was able to successfully reconstruct modulus elastograms using data obtained from magnetic resonance and x-ray computed systems.
(b) Gradient-based optimization method
Although the gradient can be computed using the method described in (Kallel and Bertrand, 1996), the computational expense required to compute the Jacobian matrix (i.e., the gradient) increases in proportion to the number of parameters. Oberai et al. (2003) were the first to demonstrate that this limitation could be circumvented by using the adjoint method to compute the gradient of the objective function. To do this, they added a scalar, L, (i.e., the Lagrangian) to equation (26) to produce a new objective function, which was defined as:
| (31) |
where w is the adjoint displacement field (i.e., a vector of Lagrangian multipliers). Note that L is a function of u, w and . Equations (26) and (31) are equivalent (i.e., when wT (Ku – f )=0 is satisfied for an arbitrary value of w. The change in L denoted by δ L , due to small changes in u, w and , denoted by δ u,δ w and , is given by:
| (32) |
Since equation (32) is valid for any u and w, these vectors were chosen so that the terms multiplying δ u and δ w were zero, which gives:
| (33) |
With these choices, δ L reduces to:
| (34) |
Since δπ = δL this yields:
| (35) |
where the terms in the parentheses are equal to the gradient vector, G . Computing the gradient vector requires only two forward solves: (1) to compute w i.e., solving equation (33), and (2) to compute u.
(c) Gradient-free optimization methods
In principle, we can use the generalized Hooke’s law to compute shear modulus directly from the axial strain; however, the principal stress components cannot be measured in vivo, an issue that (Ponnekanti et al., 1995) attempted to solve using the analytic method described in (Love, 1929). Given the limitations of computing stress using analytical models, Doyley et al. (1996) and then later Samani et al. (2001), used the finite-element method to compute the principal components of the stress tensors iteratively as follows (Samani et al., 2001; Doyley et al., 1996; Ponnekanti et al., 1995):
| (36) |
where is the measured strain, ν is Poisson’s ratio, and σ11, σ22, and σ33 are normal stress tensors. More specifically, modulus is assumed to be constant at the start of the reconstructive process. The modulus is updated by combining the measured axial strain with the principal stress components (i.e., σ11, σ22, and σ33) that were computed by solving the direct problem with the current estimate of Young’s modulus. Samani et al. (2001) were the first group to demonstrate that imposing geometrical constraints enhanced the performance of modulus elastograms. More specifically, they showed that dividing the reconstruction field of view (ROI) into segments based on anatomical features, then computing the average Young’s modulus over each segmented region, produced more stable elastograms.
Baldewsing et al. (2006) applied this technique to reconstructive intravascular ultrasound elastography. More specificially, they segmented strain elastograms into different segments using deformable curves, and reconstructed the shear modulus within each segment using a combination of FMINCON and Sepran (Sepra Analysis, Technical Univeristy Deflft, The Netherlands)(Baldewsing et al., 2005b) finite element packages. They demonstrated the feasibility of their technique using simulated and thin-cap fibroatheromas (TCFAs) as well as to in vivo and in vitro human coronary plaques (Baldewsing et al., 2005b).
Le Floc’h et al. (2009) also constrained their inversion approach using structural information which they obtained by segmenting radial strain obtained from coronary arteries using equation (25). Figure 6 shows examples of modulus elastograms recovered from excised tissues using their technique.
Figure 6.
caption. Sonograms, radial strain, and modulus elastgraphy obtained from homogenous and heterogenous vessel phantoms. The modulus elastgrams were reconstructed with a constrained inversion scheme. Courtesy of Drs. S. Le Floc’h, J. Ohayon, and G. Cloutier, University of Montreal Department of Radiology.
Stochastic methods, such as with genetic algorithms (GA) have also been proposed for solving the inverse problem (Zhang et al., 2006; Khalil et al., 2005). Stochastic methods can find the global minimum of the objective function without imposing any additional constraints; therefore, this reconstruction approach strategy may prove useful.
4.2 Harmonic elastography inversion schemes
Harmonic elastography can produce absolute modulus elastograms when all components of internal tissue motion are readily available. Consequently, this method is the most established MR elastographic imaging approach. Like their quasi-static counterpart, modulus elastograms are reconstructed using either direct or iterative inversion schemes. Harmonic elastography can measure modulus directly from shear speed estimates via equation (2). However, measuring shear speed in organs with complex geometries or when the propagating wave is reflected internally is challenging as discussed in section 2.2. Nevertheless using equation (8), we can properly account for complex geometries and edge reflection given appropriate discretization of the solution domain. Consequently, a variety of model-based inversion methods have been propose for harmonic MRE.
4.2.1 Direct inversion
Skinus et al. (2000) solved the inverse harmonic elastography problem using a linear system of PDE that they derived by solving the wave propagation model described in (Landau et al., 1986) in the frequency domain, and expressed Young’s modulus as a symmetric tensor. Lorenzen et al. (2003) used this inversion scheme to demonstrate that MRE can detect changes in breast tissue elasticity during the monthly hormonal cycle. Using the medical standard, the first day of menses is counted as day 1 in the woman’s cycle. Using MRE, (Lorenzen et al., 2003) showed that on day 5, the median value of elasticity for fibroglandular adipose tissue declined significantly, but at day 14, the same tissue’s elasticity increased noticeably.
Manduca et al. (2001) proposed to solve the inverse harmonic elastography problem using a direct inversion scheme, which they referred to as algebraic inversion of differential equation (AIDE). By assuming local homogeneity, the equations were solved separately at each pixel using only data from a local neighborhood to estimate local derivatives as described in (Oliphant et al., 2001). Very encouraging phantoms and patient results have been obtained using this technique. However, the large difference in magnitude of shear modulus and the second Lamé coefficient (i.e., kPa for shear modulus and GPa)prevents simultaneous estimation ofμ and λ , Manduca et al. (2001) assumed that the divergence of the displacement vector in equation (8) was negligible (i.e., ∇ · u ≈ 0). Using this assumption, μ was estimated from a single component of motion as follows:
| (37) |
Romano et al. (1998) developed a direct-inversion method by using the variational or weak-form of equation (8), and appropriately chosen test functions to estimate both Lamé constants. The advantage of using the weak form of equation (8) is that the derivative is calculated not from the measured data, but rather from a smooth test function.
Park and Maniatty (2006) also described a direct-inversion scheme for reconstructing shear modulus from displacements measured during time-harmonic excitation. Their approach assumed that the time-harmonic displacements were divergence-free, which reduces the governing equation to:
| (38) |
If the gradient of the shear modulus is also neglected, equation (38) reduces to the Helmholtz equation.
4.2.2 Iterative inversion method
Like its quasi-static counterpart, shear modulus can also be computed by treating the image-reconstruction problem as a parameter-optimization problem. However, to accosmplish this all component of the internal tissue displacement must be known. Using computer simulation, Van Houten et al. (2001) demonstrated that the displacement fields of an oscillating, 3D, isotropic, linear elastic body was not acurately characterized using 2D plane approximation. Consequently, no ultrasonic methods have been proposed to solve the inverse-harmonic-elastographic problem because without symmetries, the three dimensional case cannot be approximated.
The objective function to be minimized is identical to that used in the quasi-static elastography equation (29). However, the computational overhead required to solve the full 3D elasticity problem at the resolution MR data set with the Hessian method would make the computations infeasible on contemporary processors. For example, if a typical MR displacement data set were discretized to 16 × 256 × 256 image slices, the corresponding parameter set matching the MR resolution would have over a million elements (assuming a description based on single parameter of elasticity). Each parameter update for this large property description would require over ≈ 1e18 floating-point operations to invert the Hessian matrix, and an additional 1e18 operations to generate the matrix beforehand. Van Houten et al. (2001) demonstrated that this issue can be circumvented by dividing the reconstruction field-of-view into a series of overlapping subzones, and expanding equation (29) as a sum over all the subzones as follows:
| (39) |
where uz (μz ) represents the displacements on the zth subzone computed by solving the direct problem from the shear modulus (μz ), and represents the corresponding MR measured tissue displacements. They assumed that minimizing the sum in equation (39) was equivalent to the sum of minimization of the individual subzones:
| (40) |
which involves equating derivatives of displacements with respect to subzone shear modulus to zero, and solving the resulting set of nonlinear equations with the Gauss-Newton method. The resulting matrix solution at iteration ( i+1 ) has the form:
| (41) |
where represents the Jacobian matrix for a given subzone, and αz is the regularization parameter on the subzone level. Van Houten et al. (2001) deployed the subzones in a random and overlapping manner from a diminishing list of seed points that corresponded to locations in the computational domain that had n not been previously updated; however the manner in which the subzones are deployed is not essential as demonstrated in (Doyley et al., 2007). When the shear modulus at all locations is updated, a global sweep is concluded and the process is repeated. Doyley et al. (2007) demonstrated that the computatiional load of this inversion technique increased linearly with increasing subzones — a limitation that they circumvented by reducing the size of the reconstruction field of view and the overlap between subzones. Doyley et al. (2005) also demonstrated that the spatial resolution of elastograms computed using this technique was on the order of 5 mm. Figure 7 shows a representative example of an elastogram obtained from a health volunteer using the subzone-inversion technique, which illustrates that the resolution of the elastograms was sufficiently high to visualize fibroglandular tissue from the adipose tissue. The advantage of this inversion scheme is that it is ideally suited for a parallel-computing platform, because the sub-domain discretizations are computationally independent as demonstrated in (Doyley et al., 2005).
Figure 7.
Montage of MR magnitude images (A) and shear modulus elastograms (B) recovered from a healthy volunteer using the subzone inversion scheme. Courtesy of Drs. J. B. Weaver and K. D. Paulsen, Dartmouth College, Thayer School of Engineering.
Van Houten et al. (2003) reported results of a pre-clinical study that they performed on five healthy volunteers. Their results demonstrated that the elastic properties of the breast fibro-glandular and fatty breast tissues, measured in in vivo with the subzone inversion technique, were comparable to those reported in literature.
5. Advanced reconstruction methods
Soft tissues display several biomechanical properties, including viscosity, nonlinearity, porosity, anisotropy and permeability, which may improve the diagnostic value of elastography when visualized alone or in combination with shear modulus. Krouskop et al. (1998) demonstrated that clinicians could use mechanical nonlinearity to differentiate between benign and malignant breast tumors. They performed mechanical tests on excised breast tissue, which revealed that benign breast tumors displayed linear mechanical behavior, while malignant breast tumors exhibited nonlinear mechanical tendencies. There is mounting evidence that other mechanical parameters, namely viscosity (Qiu et al., 2008; Sinkus et al., 2005b), anisotropy (Sinkus et al., 2005a), and porosity can also differentiate between benign and malignant tissues – similar claims have also been made for shear modulus (Sinkus et al., 2005a). Not only can these mechanical parameters discriminate between different tissue types, but they may provide value in other clinical areas, including brain imaging (Hamhaber et al., 2010; Sack et al., 2009), distinguishing the mechanical properties of active and passive muscle groups (Asbach et al., 2008; Hoyt et al., 2008; Perrinez et al., 2009), characterizing blood clots (Schmitt et al., 2007), and diagnosing edema (Righetti et al., 2007a). Several investigators are actively developing model-based techniques to visualize different mechanical properties, either alone or in combination, using quasi-static, harmonic, and transient elastographic imaging approaches.
In the proceeding subsections, we review several promising model-based, elastographic imaging approaches that have been proposed for visualizing other biomechanical parameters besides shear modulus.
5.1 Viscoelasticity
In most approaches to model-based elastography, the mechanical behavior of soft tissues is modeled using the theory of linear elasticity (Hooke’s law), which is an appropriate model for linear elastic materials (i.e., Hookian materials). However, it is well known that most materials, including soft tissues, deviate from Hooke’s law in various ways. Materials that exhibit both fluid-like and elastic (i.e., viscoelastic) mechanical behavior deviate from Hooke’s law (Fung, 1981). For viscoelastic materials, the relationship between stress and strain is dependent on time. Viscoelastic materials exhibit three unique mechanical behaviors: (1) strain increases with time when stress (externally applied load) is sustained over a period of time, a phenomenon that is known as viscoelastic creep; (2) stress decreases with time when strain is held constant, a phenomenon known as viscoelastic relaxation; (3) during cyclic loading, mechanical energy is dissipated in the form of heat.
Viscoelastic materials are usually characterized by suddenly applying a uniform stress or strain that is sustained over a period of time. Several investigators have proposed elastographic imaging methods as a way to visualize the mechanical parameters that characterize linear viscoelastic materials (i.e., viscosity, shear modulus, Poision’s ratio). Such methods usually involve fitting dispersive shear-wave speed and attenuation coefficients to a rheological model, such as the Voigt, Kelvin or Maxwell model.
5.1.1 Quasi-static methods
Sridhar et al. (2007a, b) developed an elastographic imaging approach for characterizing viscoelastic materials. More specifically, they acquired time-varying axial strain elastograms when a viscoelastic material was subjected to a constant stress, and constructed a creep curve at each pixel from the time-varying strain elastograms. They computed the creep compliance from the the ratio of the time-varying strain, ε (t) , to the applied stress; and computed the complex compliance, D*(s) , from the Laplace transform of the creep compliance:
| (42) |
where D’(s) and D” (s) represent the storage and loss compliance, respectively. Sridhar et al. (2007a) used a three-parameter Kelvin-Vogit rheological model to predict the strain response at each pixel within the time-varying strain elastogram. In the time domain, the resulting strain response is given by:
| (43) |
where εo is the instantaneous strain, i.e., the strain incurred immediately after compression; ε1 is the viscoelastic strain amplitude; and t1 is the retardation time, i.e., the time required for the tissue to become fully deformed. They estimated the three model pameters by fitting the rheological model to the measured creep response at each pixel. Using this tecnique, this group demonstated that t1 is the most useful parameter for discriminating between malignant and benign breast tumors (Qiu et al., 2008). More specifically, t1 values measured from malignant tissue were smaller than those measured from the surrounding healthy breast tissue; whereas, the converse was observed for benign tumors.
5.1.2 Harmonic methods
Hoyt et al. (2008) proposed a viscoelastic approach based on sonoelastography imaging. They measured the visoelastic properties of gelatin and muscle samples, by fitting a Voigt model to the dispersive shear speed obtained using the crawling-wave method described in (Wu et al., 2006). These authors validated their technique by conducting simulations, phantom studies, and human studies. The simulation studies revealed a 2.3 % difference in the computed and true shear speeds under ideal measurement conditions. The phantom studies revealed a 1 % error in shear modulus that had been computed using the proposed technique, relative to that measured using a mechanical testing system. They also observed a slight increase in shear speed with increased frequency. Statistically significant differences were observed in the shear and loss moduli of relaxed and volunteered contracted muscles. The authors also observed a slight increase in shear speed with frequency. To minimize any anisotropic effects, they obtained data parallel to the muscle fiber.
Asbach et al. (2008) used their multifrequency MR elastography method to measure the viscoelastic properties of normal liver tissue versus diseased liver tissue taken from patients with grade 3 and 4 liver fibrosis. Like Hoyt et al. (2008), they measured shear-wave and shear-attenuation dispersion; but, rather than using ultrasound, they computed shear wave and shear attenuation from the Fourier transform of the complex MR displacement fields. They computed the shear modulus and viscosity variations within the tissue by fitting a Maxwell rheological model to the measured data, by solving the linear viscoelastic wave equation in the frequency domain. They observed that fibrotic liver tissue had a higher viscosity (14.4 ± 6.6 Pa s) and elastic modulus (μ1 = 2.91 ± 0.84kPa and μ2 = 4.83 ± 1.77kPa) than normal liver tissue. Their results revealed that although liver tissue is dispersive, it appeared as non-dispersive between the frequency range of 25 — 50 Hz. This research group has also measured the viscoelastic properties of brain tissues (Hamhaber et al., 2010; Sack et al., 2009), but in that case, they characterized the viscous properties of the brain by fitting a Voigts model to measured complex modulus. They also observed that the viscosity didn’t agree with the predictions of the Kramers-Kronig relation (Klatt et al. , 2010; Madsen et al., 2008; Urban and Greenleaf, 2009). Klatt et al. (2010) also measured the viscoelastic properties of the liver. In this case, the spring-pot model was used to study the dispersive behavior of the viscoelastic properties between frequency ranges of 25, 37.5, 50 and 62.5 Hz. Like Hoyt et al. (2008), they observed that the stiffness and viscosity of muscle increased with voluntary contraction.
5.1.3 Transient methods
Catheline et al. (2004) were the first to propose a method to visualize the viscoelastic properties of soft tissues. Using transient elastography, they measured the spatial variation of the time-harmonic displacement field, and used a plane-wave approximation to compute the complex wave number ( k = k’ + iαT ) of the propagating waves, as follows:
| (44) |
where uz(x) is the measured displacement, and FT is the Fourier Transform. The wave speed and attenuation coefficients of the propagating shear wave relate to the complex wave number as follows:
| (45) |
where 𝕽 and 𝕵 represents the real and imaginary component of the complex wave number, respectively.
Catheline et al. (2004) used Agar-gelatin phantoms to demonstrate that the shear wave speed ( c2 ) and attenuation coefficient (αT ) computed using equation (45) were comparable to those measured independently from phase and amplitude measurements. They computed the shear modulus (μ ) and viscosity (η ) by fitting the measured speed of sound and attenuation to Voigt’s and Maxwell’s rheological models, whose wave speed and attenuation were given by:
| (46) |
and similarly, the attenuation was given by:
| (47) |
where the superscripts V and M represent the Voigt and Maxwell models, respectively. The recovered shear modulus values were independent of the rheological model employed, but researchers observed an order of magnitude difference in viscosity values recovered with the two models. This was not surprising, because the goodness of fit of the wave-speed dispersion data to both rheological models were comparable, but Catheline et al. (2004) had demonstrated that the Voigt model provided a better fit to the attenuation-dispersion data than the Maxwell model, which proved that attenuation coefficents were independent of frequency despite the strong frequency dependency that was apparent in the data. Catheline et al. (2004) also had conducted studies on excised bovine muscles, which revealed two apparent wave speeds: either a fast or a slow wave was observed, depending on the polarization. They obtained a good estimate of both wave speeds using equation (46), but there was an overestimation of attenuation, because the model assumed the displacement field arose solely from transverse waves.
Sinkus et al. (2005b) developed a direct-inversion scheme to visualize the mechanical properties of visocelastic materials, in which a curl operation was performed on the time-harmonic displacement field u(x, y,z,t) = u(x, y,z)ejωt to remove the displacement contribution of the compressional wave. They dervived the governing equation that describes the motion incurred in an isotropic, viscoelastic medium by computing the curl of the PDEs that describe the motion incurred by both transverse and compressional shear waves. The resulting PDEs for transverse waves are given in compact form by:
| (48) |
Sinkus et al. (2005b) developed a direct-inversion scheme from equation (48), in which μ and η (viscosity) were the unknowns. They evaluated the inversion scheme using (a) computer simulations, (b) phantom studies, and (c) patient studies. Their simulation studies revealed that the proposed algorithm could accurately recover shear modulus and viscosity from ideal displacement data. However, with noisy displacements, a good estimate of shear modulus was obtained only when the shear modulus of the simulated tissue was < 8 kPa; the inversion scheme overestimated the shear modulus values when actual stiffness of the tissue was larger than 8 kPa. A similar effect was observed when estimating viscosity, albeit much earlier (i.e., the algorithm provided good estimates of of viscosity when μ < 5 kPa). Although the shear modulus affected the bias in the viscosity measurement, the authors demonstrated that the converse did not occur; i.e., the viscosity did not affect the bias in shear modulus. Despite these issues, their phantom studies revealed that inclusions were discernible in both μ and η -elastograms, and the viscosity values agreed with previously reported values for gelatin (0.21 Pa s). The patient studies revealed that the shear modulus values of malignant breast tumors were noticeably higher than those of benign fibroadenomas, but there was no significant difference observed in the viscosity of the tumor types, a result that would appear to contradict those reported in (Qiu et al., 2008).
Vappou et al. (2009) proposed a two-step approach for quantifying the viscoelastic properties of tissue. They measured the real component of the wave number (k’) from the phase ( ϕ) of the Fourier transform of the time-varying displacement at the excitation frequency:
| (49) |
They also measured the ratio of the real to the imaginary component of the complex shear modulus, from the phase between shear strain images and radiation force:
| (50) |
From R and k’ , they computed the k” (the imaginary component of the complex wave number) using the following relation:
| (51) |
Using this relation, they computed the storage ( G’(ω ) ) and the loss ( G”(ω )) as follows:
| (52) |
They validated their technique by performing phantom studies, and observed good agreement between the storage moduli that had been computed with the proposed technique, and those that had been measured with a commercially available rheometer. However, there was large discrepancy between the loss moduli.
Schmitt et al. (2010) used a similar approach to characterize the viscoelastic properties of vascular tissues. In their approach, they computed the real and imaginary components of the complex wave number from the Fourier transform of the real component of the complex time-harmonic displacement (i.e., u(x, y,t) = u ei(k’+jαT) o eiϕ ). They computed the attenuation coefficient by fitting a line to the natural log of the absolute value of the complex time-harmonic displacement. Storage and loss moduli were computed using using equation (60) as described in (Vappou et al., 2009), where k” = α . For materials with vascular geometries, they fitted the complex modulus that was computed using an analytic model to the measured data, using MATLAB’s nonlinear solver. They measured the dispersion of G’ and G” in aortic samples between 540-670 Hz, and conducted experiments on rat liver where G’(ω ) and G”(ω ) were 119.24 ± 61.6 Pa and 96.7 ± 7.9 Pa, respectively, at 250 Hz. The group also demonstrated that the viscoelastic properties of blood clots could be characterized using the proposed technique. However, in these studies of complex moduli, they estimated the storage and loss moduli by fitting a rheological model to the measured data. More specifically, they compared the goodness of fit of five rheological models—Maxwell, Kelvin-Voigt, Jeffery, Zener, and a third-order Maxwell—and observed that the Zener model gave the best fit to the data. G’ had the maximum chang at the beginning, and stabilized after 120 minutes; whereas G” was constant, with a spike between 38 and 81 Hz, followed by a gradual decrease in amplitude.
5.2 Poroelasticity
Poroelastic materials also display a transient mechanical response (i.e., they display creep and stress relaxation when a load is applied and is held constant for a while). This is a phenomenon that occurs because the matrix of poroelastic materials is porous, and interstitial fluid may flow through the pores when a load is applied. Multi-phasic mechanical models are typically used to predict the temporal mechanical response of poroelastic materials. These mechanical models assume that poroelastic materials consist of two or more distinct phases. For example, the biphasic mechanical model described in Armstrong et al. (1984) assumes that poroelastic materials consist of both a solid and a fluid phase, and that the material’s transient behavior is governed by the interaction of the two phases, i.e., the mechanical properties of the solid matrix and the permeability of the matrix to fluid. Although porous and viscoelastic materials both exhibit transient mechanical behavior, the porous material is compressible, whereas the viscoelastic material is incompressible. More specifically, volume is conserved when viscoelastic materials are deformed, but this is not the case for poroelastic materials.
Poroelastic models, such as the biphasic model described in Armstrong et al. (1984) and the consolidation mechanical model described in (Miga et al., 2000), have been used to model the transient response of brain tissue, cartilage, and other soft tissues. It has also been demonstrated that the mechanical behavior of pathological conditions, such as edema, may be described with a poroelastic model, and elastography could be extended to allow visualization of the poroelastic mechanical parameters — important information that may be used to characterize and monitor the treatment of edema (Righetti et al., 2007a). Consequently, several groups are now actively developing methods to extend both ultrasound and MR elastography to poroelastic materials.
5.2.1 Quasi-static methods
Konofagou et al. (2001) introduced poroelastography. Using the finite-element method, they studied the temporal behavior of the radial-to-axial strain ratio within a homogenous, cylindrically shaped poroelastic material during stress relaxation. They predicted that three mechanical responses would be seen in poroelastic materials; specifically, that:
(a) The radial-to-axial strain ratio elastograms would have a uniform value of 0.5 immediately after compression, which was consistent with the theoretical predictions made earlier by Armstrong et al. (1984) using an analytical model.
(b) The radial-to-axial strain ratio within the sample would tend towards an equilibrium value that was equal to the Poisson’s ratio of the solid matrix (νs ) when the compression was sustained.
(c) The time taken to reach equilibrium (the time constant) would depend on permeability of the solid matrix and the length of the fluid path — i.e., that materials with a high permeability would reach equilibrium more quickly than materials with a low permeability.
Righetti et al. (2004) demonstrated the feasibility of poroelastography experimentally. By studying the transient mechanical behavior of drained and undrained tofu samples (Wu, 2001), Righetti and colleagues demonstrated the following transient mechanical behaviors: (1) the mean radial-to-axial strain ratio of undrained tofu samples was approximately 0.5 immediately after compression, which was consistent with the numerical predictions of Konofagou et al. (2001); (2) the mean radial-to-axial strain ratios of drained and undrained tofu samples were noticeably different, but no significant difference was observed in rehydrated and undrained tofu samples; (3) the mean radial-to-axial strain ratio of undrained tofu samples decayed from 0.5 towards an equilibrium value that was slightly higher than Poisson’s ratio measured for the drained state; however, the rate of decay of the measured radial-to-axial strain ratio was noticeably slower than that predicted by the analytical model described in (Armstrong et al., 1984); and finally, (4) the mean radial-to-axial strain ratio of drained tofu samples displayed some transient mechanical behavior, albeit only slight, which suggests that besides being porous, the tofu samples were also viscoelastic.
Berry et al. (2006a) derived analytical expressions to predict the internal strain field of cylindrically shaped poroelastic materials that are undergoing stress relaxation. By extending the analytical model described in (Armstrong et al., 1984), they derived analytical expressions for predicting the spatio-temporal behavior of radial strain, axial strain, and radial-to-axial strain ratio elastograms. Using the derived equations, they predicted that immediately after compression, the radial-to-axial strain ratio would be equivalent to 0.5, and both the radial-to-axial ratio would decay to towards an equilibrium value that is equal to the Poisson’s ratio of the solid matrix when compression is sustained. This theoretical prediction was consistent with that predicted by Konofagou et al. (2001) using the finite-element method. They also demonstrated that there was good agreement between the mean radial-to-axial strain ratio predicted using the derived equation and those computed using either the analytical model described in (Armstrong et al., 1984), or the finite-element method. Using the modified analytical model, Berry et al. (2006a) predicted two mechanical behaviors that were not previously reported. More specifically, they predicted that (1) a plateau would be present in the radial-to-axial strain ratio profile in the early stages of stress relaxation, because fluid flow does not begin simultaneously throughout poroelastic materials; and that (2) near the surface, the radial-to-axial strain ratio would overshoot the Poisson’s ratio of the matrix analytical model to the time-dependent strain elastograms.
In a companion paper, Berry et al. (2006b) reported the results of experiments that they had performed to corroborate both the theoretical predictions reported in Berry et al. (2006a), and predictions made using the finite-element method concerning the effect of non-slip boundary conditions on the strain response within a poroelastic material undergoing stress relaxation. Using the finite-element method, they predicted that the transient strain response of cylindrically shaped poroelastic materials with slip boundary conditions would be noticeably different from those observed in samples with non-slip boundary conditions. More specifically, they predicted that: (1) immediately after compression and at equilibrium, region variations would be present in the radial, axial, and radial-to-axial strain elastograms obtained from poroelastic materials with non-slip boundary conditions; (2) axial strain elastograms would be time-dependent and spatially varying, because during stress relaxation, the axial strain in the central region would transfer to regions near non-slip boundaries; and (3) radial-to-axial strain profiles acquired from regions far away from the nonslip boundaries would be similar to those acquired for samples with slip boundary conditions. Berry et al. (2006b) also introduced a new elastogram known as the volumetric strain elastogram, which was the most useful elastogram for studying the transient mechanical behavior of poroelastic materials. They showed that, immediately after compression, this parameter was zero (incompressible) for samples with slip and non-slip boundary conditions. Although their experimental results departed from the theoretical predictions, they demonstrated that useful parametric images could be obtained experimentally using their model-based reconstruction approach. However, this approach was not without problems; local variations were observed in the parametric images obtained from a homogeneous sample, but the results were sufficiently encouraging to warrant further investigation.
The main limitations of stress-relaxation studies are that temporal variation is not typically observed in the axial direction during unconfined testing, and that the poor lateral resolution of current ultrasound systems compromises the quality of radial-to-axial strain elastograms. To address this issue, Righetti et al. (2007b) studied the temporal behavior of porous materials during creep. They demonstrated that the quality of transient axial strain elastograms was sufficiently high to differentiate between various grades of tofu samples. They generated time-constant elastograms by fitting an exponential function to each pixel in the time-sequence axial-strain elastogram. Using this technique, they demonstrated that they could detect focal poroelastic inclusions embedded in a poroelastic background with a contrast-to-noise ratio.
5.2.2 Harmonic Methods
Poroelasticity has also been explored using steady-state harmonic magnetic resonance elastography (Perrinez et al., 2010). More specifically, Perrinez et al. (2010) described a novel, 3D inversion scheme for recovering the mechanical parameters from volumetric displacement data obtained with MR in a porous media. They formulated the inverse-elasticity problem by treating it as a parameter-optimization problem, in which the goal was to minimize the difference between (1) measured displacements and (2) those computed by solving the partial differential equations that describe time-harmonic behavior of a poroelastic medium, which is composed of a porous, compressible, linear elastic solid matrix and a viscous, incompressible fluid. The resulting system of PDEs that describes the forward problem is given by:
| (53) |
The parameter β is defined as:
| (54) |
where p is the time-harmonic pore pressure; κ is the hydraulic conductivity; ϕ is the matrix porosity; and ρf and ρa represent the pore-fluid density and the apparent mass density, respectively.
Minimizing the objective function with respect to Lamé constants is a nonlinear process that can be solved using the Gauss-Newton iterative scheme. At each iteration, updates to the mechanical parameters are computed as follows:
| (55) |
where {δδ } = {δμ,δλ, δp}, J*T J is the self-adjoint Hessian matrix, α is the regularization parameter, J* is the complex Jacobian or sensitivity matrix, and um and uc are the measured and computed displacement fields, respectively.
Perrinez et al. (2010) solved equation (55) using the sub-zone inversion approach described in (Van Houten et al., 2001; Van Houten et al., 1999), which they implemented on a parallel-computing platform as described in (Doyley et al., 2004). They performed simulation and phantom studies to assess the performance of the proposed algorithm. The simulation study revealed that the algorithm could recover good elastograms (i.e., shear modulus, the second Lamé constant, and pore-pressure amplitude) in the presence of 5% additive noise, and that hydraulic conductivity influenced the performance of the reconstruction method. More specifically, the reconstruction method overestimated shear modulus when image reconstructions were performed using hydraulic conductivity less than 1×10−9, and considerable variability was observed in recovered images when hydraulic conductivities were greater than the true values. Perrinez et al. also performed a phantom study to assess the performance of the poroelastic reconstruction method relative to the linear-elastic reconstruction method described in (Van Houten et al., 2001; Van Houten et al., 1999; Doyley et al., 2004) . In this study, they perfoormed MR elastographic imaging on a phantom that contained a cylindrically shaped gelatin inclusion that was embedded in a block of tofu. Elastograms recovered with the linear -elastic inversion scheme showed high variations of the recovered shear modulus in both the surrounding poroelastic background and the linear elastic inclusion; whereas, the poroelastic-inversion scheme produced noticeably better images.
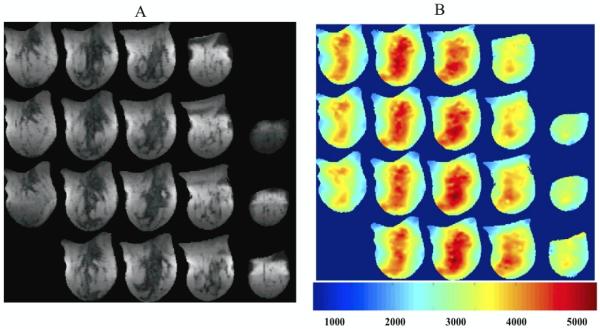
The advantage of the poroelastic inversion scheme as a reconstruction method is that it produces images of the pore-pressure that could prove useful in studying edema or hydrocephalus. Figure 8 shows examples of poroelastic elastograms obtained from the brain of a healthy volunteer using the poroelastic inversion scheme described in (Perrinez et al., 2010).
Figure 8.
Shear images (a) and pore-pressure images (b) showing 16 coronal slices through the brain. Images cover most of the ventricles, which are depicted by the lower shear modulus (blue inn image 10a). Voxel size was 3.0 mm3. Courtesy of Drs. J. B. Weaver and K. D. Paulsen, Dartmouth College, Thayer School of Engineering.
5.3 Nonlinearity
Soft tissues display nonlinear mechanical behavior because of geometric and/or material nonlinearity as discussed in (Taber, 2004).
5.3.1 Geometric nonlinearity
When soft tissues deform by a small amount (an infinitesimal deformation), their geometry in the undeformed and deformed states is similar, and thus the deformation is characterized using engineering strain. However, when soft tissues experience a finite deformation, their geometries are noiceably different in the undeformed and deformed states. In such cases, errors are incurred when deformations are significantly different; thus, engineering strain provides an accurate measure of the deformation. To characterize finite deformation, we first have to define a reference configuration, which is the geometry of the tissue under investigation in either the deformed or undeformed state. The Green-Lagrangian strain tensor can be used to characterize the deformation incurred during finite deformations, which is defined as:
| (56) |
The nonlinear term is neglected when the magnitude of the spatial derivative is small, to produce the linear strain tensor as defined in equation (6). The relationship between stress and strain is nonlinear even for a linearly elastic material when it is undergoing finite deformations. Conseqently, Skovoroda et al. (1999) proposed an iterative technique to compute shear modulus for materials undergoing finite deformations.They performed studies using a linear elastic phantom that was undergoing finite deformation, to evaluate the quality of the ensuring elastograms relative to those produced using equation (22). The results of this investigation revealed that a smaller standard deviation was incurred in elastograms computed using the nonlinear reconstruction method for large deformations, versus elastograms computed using the linear-elastic reconstruction method (i.e., based on equation (22)).
5.3.2 Material nonlinearity
Some materials exhibit nonlinear material properties that are typically described using a strain energy density function. Among the strain engery functions proposed in the literature, the most widely used for modeling tissues are (a) the Neo-Hookean hyperelastic model, and (b) the Neo-Hookean model with anexponential term. Oberari et al. (2009) used a different model, the Veronoda-Westman strain energy density function, to describe the finite displacement of a hyperelastic solid that is undergoing finite deformation, which is defined by:
| (57) |
where the terms I1 and I2 are the first and second invariants of the Cauchy-Green strain tensor, μ0 is the shear modulus, andΓ denotes the nonlinearity. The authors proposed to produce a secant modulus elastogram, by minimizing the following function:
| (58) |
Where ϑ is the total variation diminishing (TVD) regularization functional. For the nonlinear case, they proposed to reconstruct a nonlinear parameter, and the shear modulus at zero strain by minimizing the following functional:
| (59) |
In this case, there were two displacements: one obtained at small strain value, denoted by and the other obtained at larger strain, denoted by ; the corresponding predicated axial displacements were denoted by u1 and u2, respectively. The weighting factors w1 and w2 were selected to ensure that both the large deformation data and the small deformation data contribute in roughly equal measures.
Equations (58) and (59) were minimized using the quasi-Newton methods (.i.e., the Broyden-Fletcher-Goldfarg-Shanno method). They compared the performance of modulus elastograms computed using the secant and nonlinear iteriative inversion techniques, using data obtained from voluteer breast-cancer patients, one with a benign fibroadenoma tumor and the other with an invasive ductal carcinoma(IDC). For the fibroadenoma case, the tumor was visible in modulus elastograms that had been computed using small strain and large strain (12 %), although the contrast of the elastograms computed at large strain (7:1) was lower than that computed at smaller strain (10:1). The fibroadenoma tumor was not visible in nonlinear-parameter elastograms. The inclusion in the patient with IDC was discerible in shear modulus elastograms recovered using small and larger strains; however, the stiffness contrast of the modulus elastograms recovered at both small and high strains were comparable, and the IDC tumor was visible in nonliear-parameter elastograms. This result is one of several that have demonstrated the clinical value of nonlinear elastographic imaging. Specifically, model-based elastography can characterize the nonlinear behavior of soft tissues and may be used to differentiate between benign and malignant tumors. Figure 9 shows examples of shear modulus and nonlinear parameter images of the breast that were computed using the nonlinear reconstruction technique.
Figure 9.
Reconstructions of the shear modulus (Mu) and the nonlinear parameter (Gamma) for breast tissue using in vivo free-hand compression data. The tissue behavior is governed by an exponential stress-strain law, where the parameter Mu represents the shear modulus at small strain, and the nonlinear parameter, Gamma, represents the exponential increase in stiffness with increasing strain. (A) and (B) are the images for a Fibroadenoma (FA), and (C) and (D) are the images for an Invasive Ductal Carcinoma (IDC). Courtesy of Dr. A. Oberai, Rensselaer Polytechnic Institute.
5.4 Anisotropy
The stiffness tensor given in equation (4) contains 21 independent coefficients; however, neither ultrasound nor MR elastography imaging technology allows us to measure all these parameters in a practical manner. Consequently, to solve this dilemma, we can use simplified mechanical models whose stiffness matrices contains fewer independent coefficients. The stiffness matrix of the simplest mechanical model currently used in elastography — a model that is valid for an elastically isotropic material — contains two independent coefficients: shear modulus (μ ), and the second Lamé’s coefficient (λ ). This model has been adequate for most tissues with the exception of muscle, however all tissues will exhibit anisotropic mechanical behavior when they are probed deeply enough, which also emphasizes the need for exploring the anisotropic model.
Several anisotropic models have been proposed to describe the mechanical behavior of polymers, in which the models depend both on the material’s crystalline morphology and the molecular orientation. The transversely anisotropic model is perhaps the simplest anisotropic model; it assumes the mechanical properties are isotropic in the plane orthogonal to the molecular orientation. The stiffness matrix of the transversely anisotropic model contains five independent coefficients; it is ideally suited for tissues containing parallel fibers, such as muscles.
Papazoglou et al. (2005) developed an analytical tool to compute the coefficients for a transversely anisotropic medium. Several groups have observed that shear waves patterns of isotropic material are concentric, while those of muscle and tendons (anisotropic materials) have V-shaped patterns (Dresner et al., 2001; Sack et al., 2002; Uffmann et al., 2004). Papazoglou et al. (2005) used an elliptical approximation of the shear waves to model the V-shape wave patten, which they derived by assuming incompressiblity from a transversely anisotropic elasticity model. Using this anlytical tool, they characterized the V-shaped wavefront in terms of its straightness, slope, and interference; they used these results to estimate the coefficient of the transverely anisotropic models. They analyzed 2-D shear wave patterns from images of human biceps, obtained via MR elastographic imaging using the proposed technique, and demonstrated that shear-wave speeds parallel to the muscle fibers were approximately four times faster than those perpendicular to the fibers.
Sinkus et al. (2005a) developed a direct inversion scheme for reconstructing the mechanical parameters of transversely anisotropic materials from time-harmonic displacement estimates obtained using MRE. They removed the dependence of Poisson’s ratio on the reconstruction procedure by applying the Helmholtz-Hodge decomposition, which states that every vector field can be written as a sum of the divergence-free part, the curl-free part, and the harmonic part. Using computer simulations, they demonstrated that the proposed inversion scheme produced good modulus elastograms in the presence of 10 % additive noise, albeit the modulus elastograms were biased. Sinkus and colleagues also conducted phantom studies to evaluate the performance of the method. They observed that they could discern hard inclusion in the shear modulus elastograms, but the magnitude of anisotropy elastograms was low owing to the absence of anisotropy in the phantom. When Sinkus and colleagues applied this technique and took images in volunteers with benign and malignant tumors, they observed enhanced anisotropic and viscous properties within the tumors.
6. Discussion
Developing elastography within the framework of solving an inverse problem should provide more accurate estimates of the mechanical parameters of human tissues than the simple approaches described in section 2 of this article. However, several concerns remain to be resolved before model-based elastography could become the prevailing approach to quasi-static, harmonic, and transient elastography. These concerns include: (1) developing practical techniques to transform ill-posed problems into a well-posed ones; (2) minimizing model-data mismatch; and (3) developing better test procedures to evaluate and optimize the performance of advanced reconstruction methods.
6.1 Transforming the reconstruction problem to a well-posed one
Solving the inverse elasticity problem may produce a non-unique solution. More specifically, both valid and invalid modulus distributions could yield identical mechanical responses. We can recognize invalid modulus distributions in cases when the truth is known (as in simulation and phantom studies), but misdiagnosis could occur if invalid modulus distributions were to masquerade as the truth. Several researchers have applied the uniqueness theorem to elastography. Barbone and Bamber (2002) found that solving the quasi-static inverse elasticity problem with one displacement field did not produce unique modulus elastograms. McLaughlin and Yoon (2004) found that transient elastography could provide unique modulus elastograms when the full 3D displacement field is available. Although the uniqueness theorem has not been applied to harmonic elastography, accurate estimates of shear modulus have been recovered with steady state harmonic elastography (Doyley et al., 2003). The author would like to caution the reader that though solving the transient elastography problem yields a unique solution for simple materials (i.e., linear, purely elastic, isotropic), there is no guarantee that this method will provide a unique solution when it is applied to soft tissues, which exhibit complex mechanical behavior (McLaughlin and Yoon, 2004). In the proceeding sub-sections, we describe strategies for introducing a priori information into the image reconstruction process that is applicable to all approaches to elastography.
(a) Regularization
The ill-pose issue occurs when pertinent information about the solution is not available; therefore, the goal of regularization is to introduce a priori information, such as smoothness, in the reconstruction process. The two challenges we may encounter when using regularization are (i) selecting the most appropriate method, and (ii) deciding the optimum value of the regularization parameter. Too little regularization produces unusable modulus elastograms, while excessive regularization typically produces low-resolution modulus elastograms.
Discovering the most appropriate regularization technique for elastography is still an open research question, but the Tikhonov regularization is currently the most commonly used method. From our experience, elastograms produced with the total variation diminishing (TVD) regularization method usually possess better (contrast recovery and contrast-to-noise ratio) than elastograms computed using the Tikhonov regularization method, although the TVD regularization method typically does produces blotchy images (Richards and Doyley, 2011). The H1-seminorm regularization method could prove to be a better choice, since this regularization method typically produces elastograms that do not contain “blotchy” artifacts, its performance is comparable to modulus elastograms produced with the TVD method. However, before settling on any given regularization method more detailed studies must be conducted.
Developing objective methods to select the optimum value of the regularization parameter is another concern. To avoid the temptation of “tweaking”, the regularization parameter should be selected objectively using either the L-curve or the generalized cross-validation method (Vogel, 2002). However, since the L-curve and the generalized cross valiation methods are not appropriate for clinical applications, the author recommends that a statistical approach to the image reconstuction problem be employed, since statistical-based reconstruction methods provide a precise description of the regularization parameter (Van Houten et al. 2003).
(b) Spatial priors
In addition to regularization, other methods could transform the ill posed inverse elasticity problem to a well-posed one. For example, Barbone and Bamber (2002) suggested that model-based elastography be performed with multiple, independent displacement fields. Although feasible for quasi-static breast elastography, this method would be difficult to implement in other approaches to elastography. An alternate approach is to incorporate structural information in the image reconstruction process (Richards et al., 2010; Baldewsing et al., 2006; Baldewsing et al., 2005b; Le Floc’h et al., 2009; Le Floc’h et al., 2010). Structural information can be obtained by segmenting images obtained from ultrasound, MR, or other sources. In quasi-static elastography, spatial priors are typically used to impose hard constraint on the reconstruction process through a procedure known as parameter reduction (referred to here as “hard prior reconstruction”). More specifically, the shear moduli of all pixels in a given region as defined by the spatial prior are lumped together. Hard-prior reconstruction methods do not require regularization because the reconstruction problem is well conditioned; however, the technique is prone to errors because the segmentation of congruent features may contain classification errors. The author recommends that spatial prior should be used to impose soft constraints but not hard constraints, since this should minimize the effect of segmentation errors on the reconstruction process.
6.2 The consequence of modeling errors
Errors are guaranteed to occur in model-based elastography because of (a) measurement noise, and (b) discrepancy between the model and reality. However, without additional information, we cannot distinguish between errors due to measurement noise, and errors due to a limited model. Nonetheless, if we were to consider a hypothetical case in which modeling errors exceeded the measurement noise, an important question to ask is: “how would modeling errors impact the resulting modulus elastograms?” The short answer to this question would be that it depend on the severity of the error. More specifically, the reconstruction process would produce erroneous modulus elastograms if the modeling error were severe; however, it would provide plausible modulus elastograms that might contains artifacts if the the modeling error were small, yet significant. Another important question to ask would be: “what is the consequence of using the plane strain approximation to approximate a 3D elasticity problem?” In quasi-static elastography, the plain-strain approximation does not represent a major challenge, because the motion of the tissue can be confined in the in-plane direction during imaging (Kallel et al. 1997b) — which should be consistent with the motion predicted with the plane strain elasticity model. Unfortunately, in transient and harmonic elastography, it is difficult to confine the propagation of shear waves to the in-plane direction; therefore, erroneous elastograms would be produced if image reconstruction were performed using an approximate mechanical model. Another question to ask would be “what would happen if linear elastic reconstruction methods were used to reconstruct the shear modulus of tissues that exhibit complex mechanical behavior (i.e., viscous, nonlinear, anisotropic materials)?” We have observed, when using steady state harmonic elastography (Perreard et al., 2010), that when linear elastic reconstruction was applied to frequency-dependent phantoms, the shear modulus estimates were consistently less accurate — in somewhat unpredictable ways that resulted from a complex interplay between multiple factors (i.e., size, shape and contrast of inclusions). The author expects that a similar behavior to occur if linear elastic reconstruction methods were applied to materials that exhibits strong poroelastic, anisotropic or nonlinear elastic behavior.
There is recent considerable interest in using elastography to visualize the viscoelastic behavior of soft tissues. It is also clear that if viscoelastic elastography is to become a viable clinical approach, then better mechanical models must be employed to accurately capture the viscoelastic behavior of soft tissues. The author agrees that transient and harmonic elastographic imaging is perhaps the most natural approach for viscoelastic elastography, because the harmonic solution of the wave equation can easily be transformed into a dispersive relation. By fitting a rheological model to wave-speed data and attenuation dispersion data, viscosity and shear modulus can be estimated. The problem with this approach is that although most rheological models provide good estimates of wave-speed dispersion, there is often a large discrepancy between the measured attenuation dispersion and computed attenuation dispersion. An alternative approach could be to develop a reconstruction method based on a viscoelastic continuum mechanical model, since this might provide a more accurate prediction of wave-speed and attenuation dispersion over the small frequency range employed in elastography.
Poroelasticity is another rapidly developing imaging modality. However, there is disagreement concerning the most appropriate models for poroelastic imaging of the brain and cartilage. Some researchers prefer biphasic models, while others other researchers prefer consolidation models — such as those employed in soil mechanics. Still other researchers suggests that neither biphasic nor consolidation models suffice; they believe that viscoelastic models should be used. As with viscoelastic elastography, in poroelasticity, there also needs to be consensus among the elastographic imaging community about which is the most appropriate model.
6.3 Evaluating performance
Several research groups are developing model-based elastographic imaging systems to characterize the different mechanical properties within soft tissues (i.e., shear modulus, viscosity, Poisson’s ratio, anisotropy, nonlinearity). The ability to compare image quality based upon spatial and contrast resolution must be addressed if model-based elastography is to progress beyond simple anecdotal reports. One approach towards achieving this objective is to adopt a method of x-ray mammography system characterization. The low contrast performance of modulus elastograms computed with different model-based elastographic approaches could be assessed using studies similar to those described in (Doyley et al., 2003). However, to facilitate such studies, new materials must be developed to fabricate more complex phantoms. More specifically, fabrication techniques should be developed to allow the investigators to vary each mechanical parameter over a wide dynamic range. In addition, efforts should be made to develop better mechanical testing devices – especially for harmonic and transient elastography – similar to those described in (Madsen et al., 2008). Alternatively, techniques such as time-temperature superposition could be used to extend the useful range of commercial dynamic mechanical analyzers as discussed in (Doyley et al., 2010).
Acknowledgements
This work is supported by NIH National Heart and Lungs research grant R01-HL 088523. The author would like to thank Prof. Kevin Parker in the Department of Electrical & Computer Engineering at the University of Rochester for many valuable discussions and comments on the early draft of this manuscript, and Dr. Jiang Yao in the Department of Mechanical Engineering at the University of Rochester for her useful discussions.
Appendix A.
Abbreviations & Symbols
- α
regularization parameter
- αr
regularization parameter applied to nonlinearity
- αμ
regularization parameter applied to shear modulus
- αT
absorption or attenuation coefficient
attenuation coefficient of the Maxwell model
attenuation coefficient of the Voigt model
- αz
regularization parameter applied to a zone
- Cijkl
the Christoffel rank-four tensor
- c1
velocity of the compressional wave
- c2
velocity of the shear wave
shear wave speed of the Maxwell model
shear wave speed of the Voigt model
- D *(s)
complex compliance
- D ’(s)
storage compliance
- D ”(s)
loss compliance
- Δ
del operator
- δij
Kronecker delta
- E
Young’s modulus
- ε0
instantaneous strain
- ε1
viscoelastic strain amplitude
- ε
strain tensor
- ε0
axial strain
- ε (t )
time-varying strain
- f
force vector
- ʒ
imaginary component of a complex number
- G
gradient vector
- G ’
real component of complex shear modulus (storage modulus)
- G ”
imaginary component of complex shear modulus (loss modulus)
- Γ
boundary of element
- γ
nonlinearity
- HA
aggregate modulus
- HAk
product of aggregate modulus and permeability
- h
thickness
- I
identity matrix
- I1
first variant of the Cauchy-Green strain tensor
- I2
second variant of the Cauchy-Green strain tensor
- i
iteration number
- J
Jacobian or sensitivity matrix
- j
complex number
- j ”
imaginary component of the wave number
- J *T
complex Jacobian matrix
- J *TJ
complex Hessian matrix
- K
global stiffness or coefficient matrix
- k
complex wave number
- k ’
real component of the wave number
- κ
hydraulic conductivity
- L
Lagrangian scalar
- λ
second Lamé’s coefficient
- μ
shear modulus
- μr
relative shear modulus
- μz
shear modulus in a zone
- N
number of nodes
- n̂
outward pointing normal vector
- η
viscosity
- Ω
area of finite element
- Ω
angular frequency
- p
hydrostatic pressure
- p
time-harmonic pore pressure
- Φ
phase of time harmonic displacement
- ϕ
basis function associated with element
- π
objective function
- πz
objective function within a zone
- K
real component of a complex number
- ρ
density
- ρf
pore-fluid density
- ρa
apparent mass density
- σ
three dimensional stress tensor
- T
transpose
- t
time
- t̂
Neumann boundary condition
- t1
retardation time
- um
measured displacement field
- u
computed displacement field
- uz
calculated displacement within a zone
measured displacement within a zone
- v
Poisson’s ratio
- ϑ
TVD regularization functional
- vs
Poisson’s ratio of the solid matrix
- W
Veronoda-Westman strain energy density function
- w
adjoint displacement field
- wj
displacement component
- w1
weighting factor
- w2
weighting factor
- ζ
rotational vector
Footnotes
Rhagavan (1994) used the form of Hooke’s law (i.e., σij = pδij + 2μεij), which includes a hydrostatic pressure term, p .
References
- Armstrong CG, Lai WM, Mow VC. An analysis of the unconfined compression of articular cartilage. J Biomech Eng. 1984;106:165–73. doi: 10.1115/1.3138475. [DOI] [PubMed] [Google Scholar]
- Asbach P, Klatt D, Hamhaber U, Braun J, Somasundaram R, Hamm B, Sack I. Assessment of liver viscoelasticity using multifrequency MR elastography. Magn Reson Med. 2008;60:373–9. doi: 10.1002/mrm.21636. [DOI] [PubMed] [Google Scholar]
- Baldewsing R, Mastik F, Schaar J, Serruys P, van der Steen A. Robustness of reconstructing the young’s modulus distribution of vulnerable atherosclerotic plaques using a parametric plaque model. Ultrasound Med Biol. 2005a;31:1631–45. doi: 10.1016/j.ultrasmedbio.2005.08.006. [DOI] [PubMed] [Google Scholar]
- Baldewsing R, Mastik F, Schaar J, Serruys P, van der Steen A. Young’s modulus reconstruction of vulnerable atherosclerotic plaque components using deformable curves. Ultrasound Med Biol. 2006;32:201–10. doi: 10.1016/j.ultrasmedbio.2005.11.016. [DOI] [PubMed] [Google Scholar]
- Baldewsing R, Schaar J, Mastik F, Oomens C, van der Steen A. Assessment of vulnerable plaque composition by matching the deformation of a parametric plaque model to measured plaque deformation. Ieee T Med Imaging. 2005b;24:514–28. doi: 10.1109/tmi.2005.844170. [DOI] [PubMed] [Google Scholar]
- Bamber JC, Barbone PE, Bush NL, Cosgrove DO, Doyely MM, Fuechsel FG, Meaney PM, Miller NR, Shiina T, Tranquart F. Progress in freehand elastography of the breast. IEICE Trans. Inf. Syst. 2002;E85D:5–14. [Google Scholar]
- Bamber JC, Bush NL. Freehand Elasticity Imaging using speckle decorrelation rate. vol 22. Plenum Press; New York: 1995. [Google Scholar]
- Barbone PE, Bamber JC. Quantitative elasticity imaging: what can and cannot be inferred from strain images. Phys Med Biol. 2002;47:2147–64. doi: 10.1088/0031-9155/47/12/310. [DOI] [PubMed] [Google Scholar]
- Bercoff J, Tanter M, Fink M. Supersonic shear imaging: A new technique for soft tissue elasticity mapping. Ieee Transactions on Ultrasonics Ferroelectrics and Frequency Control. 2004;51:396–409. doi: 10.1109/tuffc.2004.1295425. [DOI] [PubMed] [Google Scholar]
- Berry G, Bamber J, Armstrong C, Miller N, Barbone P. Towards an acoustic model-based poroelastic imaging method: I. Theoretical foundation. 2006a;32:547–67. doi: 10.1016/j.ultrasmedbio.2006.01.003. [DOI] [PubMed] [Google Scholar]
- Berry G, Bamber J, Miller N, Barbone P, Bush N, Armstrong C. Towards an acoustic model-based poroelastic imaging method: II. Experimental investigation. 2006b;32:1869–85. doi: 10.1016/j.ultrasmedbio.2006.07.013. [DOI] [PubMed] [Google Scholar]
- Bilgen M, Insana M. Elastostatics of a spherical inclusion in homogeneous biological media. 1998;43:1–20. doi: 10.1088/0031-9155/43/1/001. [DOI] [PubMed] [Google Scholar]
- Bishop J, Samani A, Sciarretta J, Plewes D. Two-dimensional MR elastography with linear inversion reconstruction: methodology and noise analysis. 2000;45:2081–91. doi: 10.1088/0031-9155/45/8/302. [DOI] [PubMed] [Google Scholar]
- Blackstock DT. Fundamentals of physical acoustics. John Wiley & Sons, Inc.; New York, NY: 2000. [Google Scholar]
- Brigham JC, Aquino W, Mitri FG, Greenleaf J, Fatemi M. Inverse estimation of viscoelastic material properties for solids immersed in fluids using vibroacoustic techniques. Journal of Applied Physics. 2007;101 023509-0 - -14. [Google Scholar]
- Brusseau E, Fromageau J, Finet G, Delachartre P, Vray D. Axial strain imaging of intravascular data: results on polyvinyl alcohol cryogel phantoms and carotid artery. Ultrasound Med Biol. 2001;27:1631–42. doi: 10.1016/s0301-5629(01)00451-3. [DOI] [PubMed] [Google Scholar]
- Catheline S, Gennisson J, Delon G, Fink M, Sinkus R, Abouelkaram S, Culioli J. Measurement of viscoelastic properties of homogeneous soft solid using transient elastography: An inverse problem approach. J Acoust Soc Am. 2004;116:3734–41. doi: 10.1121/1.1815075. [DOI] [PubMed] [Google Scholar]
- Chenevert TL, Skovoroda AR, O’Donnell M, Emelianov SY. Elasticity reconstructive imaging by means of stimulated echo MRI. Magn Reson Med. 1998;39:482–90. doi: 10.1002/mrm.1910390319. [DOI] [PubMed] [Google Scholar]
- Cook RD, Malkus DS, Plesha DS. Concepts and applications of finite element analysis. John Wiley & sons; 1989. [Google Scholar]
- de Korte CL, Carlier SG, Mastik F, Doyley MM, van der Steen AF, Serruys PW, Bom N. Morphological and mechanical information of coronary arteries obtained with intravascular elastography. Feasibility study in vivo. Eur Heart J. 2002;23:405–13. doi: 10.1053/euhj.2001.2806. [DOI] [PubMed] [Google Scholar]
- de Korte CL, Pasterkamp G, van der Steen AF, Woutman HA, Bom N. Characterization of plaque components with intravascular ultrasound elastography in human femoral and coronary arteries in vitro. Circulation. 2000;102:617–23. doi: 10.1161/01.cir.102.6.617. [DOI] [PubMed] [Google Scholar]
- Doyley MM, Bamber JC, Shiina T, Leach MO. Reconstruction of elasticity modulus distribution from envelope detected B-mode data. In: Levy M, et al., editors. IEEE international Ultrasonics symposium Proceedings.1996. pp. 1611–4. [Google Scholar]
- Doyley MM, Feng Q, Weaver JB, Paulsen KD. Performance analysis of steady-state harmonic elastography. Phys Med Biol. 2007;52:2657–74. doi: 10.1088/0031-9155/52/10/002. [DOI] [PubMed] [Google Scholar]
- Doyley MM, Mastik F, de Korte CL, Carlier SG, Cespedes EI, Serruys PW, Bom N, van der Steen AF. Advancing intravascular ultrasonic palpation toward clinical applications. Ultrasound Med Biol. 2001;27:1471–80. doi: 10.1016/s0301-5629(01)00457-4. [DOI] [PubMed] [Google Scholar]
- Doyley MM, Meaney PM, Bamber JC. Evaluation of an iterative reconstruction method for quantitative elastography. Phys Med Biol. 2000;45:1521–40. doi: 10.1088/0031-9155/45/6/309. [DOI] [PubMed] [Google Scholar]
- Doyley MM, Perreard I, Patterson AJ, Weaver JB, Paulsen KM. The performance of steady-state harmonic magnetic resonance elastography when applied to viscoelastic materials. Medical Physics. 2010;37:3970–9. doi: 10.1118/1.3454738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doyley MM, Srinivasan S, Dimidenko E, Soni N, Ophir J. Enhancing the performance of model-based elastography by incorporating additional a priori information in the modulus image reconstruction process. Phys Med Biol. 2006;51:95–112. doi: 10.1088/0031-9155/51/1/007. [DOI] [PubMed] [Google Scholar]
- Doyley MM, Srinivasan S, Pendergrass SA, Wu Z, Ophir J. Comparative evaluation of strain-based and model-based modulus elastography. Ultrasound in Medicine and Biology. 2005;31:787–802. doi: 10.1016/j.ultrasmedbio.2005.02.005. [DOI] [PubMed] [Google Scholar]
- Doyley MM, Van Houten EE, Weaver JB, Poplack S, Duncan L, Kennedy F, Paulsen KD. Shear modulus estimation using parallelized partial volumetric reconstruction. Ieee Transactions on Medical Imaging. 2004;23:1404–16. doi: 10.1109/TMI.2004.834624. [DOI] [PubMed] [Google Scholar]
- Doyley MM, Weaver JB, Van Houten EE, Kennedy FE, Paulsen KD. Thresholds for detecting and characterizing focal lesions using steady-state MR elastography. Med Phys. 2003;30:495–504. doi: 10.1118/1.1556607. [DOI] [PubMed] [Google Scholar]
- Dresner MA, Rose GH, Rossman PJ, Muthupillai R, Manduca A, Ehman RL. Magnetic resonance elastography of skeletal muscle. J Magn Reson Imaging. 2001;13:269–76. doi: 10.1002/1522-2586(200102)13:2<269::aid-jmri1039>3.0.co;2-1. [DOI] [PubMed] [Google Scholar]
- Fatemi M, Greenleaf JF. Ultrasound-stimulated vibro-acoustic spectrography. Science. 1998;280:82–5. doi: 10.1126/science.280.5360.82. [DOI] [PubMed] [Google Scholar]
- Fowlkes JB, Emelianov SY, Pipe JG, Skovoroda AR, Carson PL, Adler RS, Sarvazyan AP. Magnetic-resonance-imaging techniques for detection of elasticity variation. Medical Physics. 1995;22:1771–8. doi: 10.1118/1.597633. [DOI] [PubMed] [Google Scholar]
- Fung YC. Biomechanics: Mechanical properties of living tissue. Springer; New York, USA: 1981. [Google Scholar]
- Geuzaine C, Remacle J-F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. International Journal For Numerical Methods In Engineering. 2009;79:1309–31. [Google Scholar]
- Greenleaf JF, Fatemi M, Insana M. Selected methods for imaging elastic properties of biological tissues. Annual Review of Biomedical Engineering. 2003;5:57–78. doi: 10.1146/annurev.bioeng.5.040202.121623. [DOI] [PubMed] [Google Scholar]
- Hall TJ, Bilgen M, Insana MF, Krouskop TA. Phantom materials for elastography. Ieee Transactions On Ultrasonics Ferroelectrics And Frequency Control. 1997;44:1355–65. [Google Scholar]
- Hamhaber U, Klatt D, Papazoglou S, Hollmann M, Stadler J, Sack I, Bernarding J, Braun J. In Vivo Magnetic Resonance Elastography of Human Brain at 7 T and 1.5 T. Journal of Magnetic Resonance Imaging. 2010;32:577–83. doi: 10.1002/jmri.22294. [DOI] [PubMed] [Google Scholar]
- Hiltawsky KM, Kruger M, Starke C, Heuser L, Ermert H, Jensen A. Freehand ultrasound elastography of breast lesions: clinical results. Ultrasound Med Biol. 2001;27:1461–9. doi: 10.1016/s0301-5629(01)00434-3. [DOI] [PubMed] [Google Scholar]
- Hoyt K, Castaneda B, Parker KJ. Two-dimensional sonoelastographic shear velocity imaging. Ultrasound Med Biol. 2008;34:276–88. doi: 10.1016/j.ultrasmedbio.2007.07.011. [DOI] [PubMed] [Google Scholar]
- Ji L, McLaughlin JR, Renzi D, Yoon JR. Interior elastodynamics inverse problems: shear wave speed reconstruction in transient elastography. Inverse Problems. 2003;19:S1–S29. [Google Scholar]
- Jiang J, Varghese T, Brace CL, Madsen EL, Hall TJ, Bharat S, Hobson MA, Zagzebski JA, Lee FT., Jr. Young’s Modulus Reconstruction for Radio-Frequency Ablation Electrode-Induced Displacement Fields: A Feasibility Study. Ieee Transactions On Medical Imaging. 2009;28:1325–34. doi: 10.1109/TMI.2009.2015355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kallel F, Bertrand M. Tissue elasticity reconstruction using linear perturbation method. IEEE Transactions On Medical Imaging. 1996;15:299–313. doi: 10.1109/42.500139. [DOI] [PubMed] [Google Scholar]
- Kallel F, Bertrand M, Ophir J. Fundamental limitations on the contrast-transfer efficiency in elastography: an analytic study. Ultrasound Med Biol. 1996;22:463–70. doi: 10.1016/0301-5629(95)02079-9. [DOI] [PubMed] [Google Scholar]
- Kallel F, Ophir J. A least-squares strain estimator for elastography. Ultrason Imaging. 1997;19:195–208. doi: 10.1177/016173469701900303. [DOI] [PubMed] [Google Scholar]
- Kallel F, Ophir J, Magee K, Krouskop T. Elastographic imaging of low-contrast elastic modulus distributions in tissue. Ultrasound Med Biol. 1998;24:409–25. doi: 10.1016/s0301-5629(97)00287-1. [DOI] [PubMed] [Google Scholar]
- Kallel F, Varghese T, Ophir J, Bilgen M. The nonstationary strain filter in elastography .2. lateral and elevational decorrelation. Ultrasound In Medicine And Biology. 1997b;23:1357–69. doi: 10.1016/s0301-5629(97)00196-8. [DOI] [PubMed] [Google Scholar]
- Kallel F, Prihoda CD, Ophir J. Contrast-transfer efficiency for continuously varying tissue moduli: simulation and phantom validation. Ultrasound Med Biol. 2001;27:1115–25. doi: 10.1016/s0301-5629(01)00411-2. [DOI] [PubMed] [Google Scholar]
- Kallel F, Stafford RJ, Price RE, Righetti R, Ophir J, Hazle JD. The feasibility of elastographic visualization of HIFU-induced thermal lesions in soft tissues. Image-guided high-intensity focused ultrasound. Ultrasound Med Biol. 1999;25:641–7. doi: 10.1016/s0301-5629(98)00184-7. [DOI] [PubMed] [Google Scholar]
- Khalil AS, Chan RC, Chau AH, Bouma BE, Mofrad MRK. Tissue elasticity estimation with optical coherence elastography: Toward mechanical characterization of In vivo soft tissue. Annals of Biomedical Engineering. 2005;33:1631–9. doi: 10.1007/s10439-005-6766-3. [DOI] [PubMed] [Google Scholar]
- Kirkpatrick SJ, Wang RK, Duncan DD. OCT-based elastography for large and small deformations. Optics Express. 2006;14:11585–97. doi: 10.1364/oe.14.011585. [DOI] [PubMed] [Google Scholar]
- Klatt D, Friedrich C, Korth Y, Vogt R, Braun J, Sack I. Viscoelastic properties of liver measured by oscillatory rheometry and multifrequency magnetic resonance elastography. Biorheology. 2010;47:133–41. doi: 10.3233/BIR-2010-0565. [DOI] [PubMed] [Google Scholar]
- Knutsson H, Westin CF, Granlund G. Local multiscale frequency and bandwidth estimation. Image Processing, 1994. Proceedings. ICIP-94., IEEE International Conference.1994. pp. 36–40. [Google Scholar]
- Ko HJ, Tan W, Stack R, Boppart SA. Optical coherence elastography of engineered and developing tissue. Tissue Engineering. 2006;12:63–73. doi: 10.1089/ten.2006.12.63. [DOI] [PubMed] [Google Scholar]
- Konofagou E, Dutta P, Ophir J, Cespedes I. Reduction of stress nonuniformities by apodization of compressor displacement in elastography. Ultrasound Med Biol. 1996;22:1229–36. doi: 10.1016/s0301-5629(96)00147-0. [DOI] [PubMed] [Google Scholar]
- Konofagou EE, Harrigan TP, Ophir J, Krouskop TA. Poroelastography: imaging the poroelastic properties of tissues. Ultrasound Med Biol. 2001;27:1387–97. doi: 10.1016/s0301-5629(01)00433-1. [DOI] [PubMed] [Google Scholar]
- Krouskop TA, Wheeler TM, Kallel F, Garra BS, Hall T. Elastic moduli of breast and prostate tissues under compression. Ultrason Imaging. 1998;20:260–74. doi: 10.1177/016173469802000403. [DOI] [PubMed] [Google Scholar]
- Landau LD, Lifshitz EM, Kosevich AM, Pitaevski LP. Theory of elasticity. 1986. p. 187.
- Le Floc’h S, Cloutier G, Finet G, Tracqui P, Pettigrew RI, Ohayon J. Vascular imaging modulography: an experimental in vitro study. Computer Methods in Biomechanics and Biomedical Engineering. 2010;13:89–90. [Google Scholar]
- Le Floc’h S, Ohayon J, Tracqui P, Finet G, Gharib AM, Maurice RL, Cloutier G, Pettigrew RI. Vulnerable Atherosclerotic Plaque Elasticity Reconstruction Based on a Segmentation-Driven Optimization Procedure Using Strain Measurements: Theoretical Framework. Ieee Transactions on Medical Imaging. 2009;28:1126–37. doi: 10.1109/TMI.2009.2012852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lerner RM, Huang SR, Parker KJ. “Sonoelasticity” images derived from ultrasound signals in mechanically vibrated tissues. Ultrasound Med Biol. 1990;16:231–9. doi: 10.1016/0301-5629(90)90002-t. [DOI] [PubMed] [Google Scholar]
- Lerner RM, Parker KJ. Sonoelasticity images, ultrasonic tissue charactertization and echographic imaging. In: Thijssen J, editor. 7th Eoropean Communities Workshop; The Netherlands: Nijmegen; 1987. [Google Scholar]
- Lerner RM, Parker KJ, Holen J, Gramiak R, Waag RC. Sono-elasticity: medical elasticity images derived from ultrasound singals in mechanically vibrated targets. Acoustical Imaging. 1988;16:317–27. [Google Scholar]
- Lionheart W. EIT reconstruction algorithms: pitfalls, challenges and recent developments. Physiological Measurement. 2004;25:125–42. doi: 10.1088/0967-3334/25/1/021. [DOI] [PubMed] [Google Scholar]
- Lorenzen J, Sinkus R, Adam G. Elastography: Quantitative imaging modality of the elastic tissue properties. Rofo-Fortschritte Auf Dem Gebiet Der Rontgenstrahlen Und Der Bildgebenden Verfahren. 2003;175:623–30. doi: 10.1055/s-2003-39199. [DOI] [PubMed] [Google Scholar]
- Love A. The stress produced in a semi-infinite solid by pressure on part of the boundary. Philosophical Transactions of the Royal Society of. 1929.
- Lubinski MA, Emelianov SY, Raghavan KR, Yagle AE, Skovoroda AR, O’Donnell M. Lateral displacement estimation using tissue incompressibility. IEEE Transactions on Ultrasonics, Ferroelectronics and Frequency Control. 1996;43:247–55. doi: 10.1109/58.660158. [DOI] [PubMed] [Google Scholar]
- Madsen EL, Frank GR, Hobson MA, Lin-Gibson S, Hall TJ, Jiang J, Stiles TA. Instrument for determining the complex shear modulus of soft-tissue-like materials from 10 to 300 Hz. Phys Med Biol. 2008;53:5313–42. doi: 10.1088/0031-9155/53/19/004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manduca A, Dutt V, Borup DT, Muthupillai R, Greenleaf JF, Ehman RL. An inverse approach to the calculation of elasticity maps for magnetic resonance elastography. <None Specified>. 1998;3338:426–36. [Google Scholar]
- Manduca A, Oliphant TE, Dresner MA, Mahowald JL, Kruse SA, Amromin E, Felmlee JP, Greenleaf JF, Ehman RL. Magnetic resonance elastography: non-invasive mapping of tissue elasticity. Med Image Anal. 2001;5:237–54. doi: 10.1016/s1361-8415(00)00039-6. [DOI] [PubMed] [Google Scholar]
- McAleavey S, Collins E, Kelly J, Elegbe E, Menon M. Validation of SMURF estimation of shear modulus in hydrogels. Ultrason Imaging. 2009;31:131–50. doi: 10.1177/016173460903100204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCracken P, Manduca A, Felmlee JP, Ehman RL. Transient MR elastography: Modeling traumatic brain injury. Medical Image Computing and Computer-Assisted Intervention - Miccai 2004, Pt 2, Proceedings. 2004;3217:1081–2. [Google Scholar]
- McLaughlin J, Renzi D. Shear wave speed recovery in transient elastography and supersonic imaging using propagating fronts. Inverse Problems. 2006;22:681–706. [Google Scholar]
- McLaughlin J, Yoon J. Unique identifiability of elastic parameters from time-dependent interior displacement measurement. Inverse Probl. 2004;20:25–45. [Google Scholar]
- Meaney PM, Demidenko E, Yagnamurthy NK, Li D, Fanning MW, Paulsen KD. A two-stage microwave image reconstruction procedure for improved internal feature extraction. Med Phys. 2001;28:2358–69. doi: 10.1118/1.1413520. [DOI] [PubMed] [Google Scholar]
- Miga MI. A new approach to elastography using mutual information and finite elements. Phys Med Biol. 2003;48:467–80. doi: 10.1088/0031-9155/48/4/304. [DOI] [PubMed] [Google Scholar]
- Miga MI, Paulsen KD, Hoopes PJ, Kennedy FE, Jr., Hartov A, Roberts DW. In vivo quantification of a homogeneous brain deformation model for updating preoperative images during surgery. IEEE Trans Biomed Eng. 2000;47:266–73. doi: 10.1109/10.821778. [DOI] [PubMed] [Google Scholar]
- Moulton MJ, Creswell LL, Actis RL, Myers KW, Vannier MW, Szabo BA, Pasque MK. An Inverse approach to determining Myocardial Material Properties. J.Biomechanics. 1995;28(8):935–48. doi: 10.1016/0021-9290(94)00144-s. [DOI] [PubMed] [Google Scholar]
- Muthupillai R, Lomas DJ, Rossman PJ, Greenleaf JF, Manduca A, Ehman RL. Magnetic-resonance elastography by direct visualization of propagating acoustic strain waves. Science. 1995;269:1854–7. doi: 10.1126/science.7569924. [DOI] [PubMed] [Google Scholar]
- Nightingale K, McAleavey S, Trahey G. Shear-wave generation using acoustic radiation force: In vivo and ex vivo results. Ultrasound in Medicine and Biology. 2003;29:1715–23. doi: 10.1016/j.ultrasmedbio.2003.08.008. [DOI] [PubMed] [Google Scholar]
- O’Donnell M, Skovoroda AR, Shapo BM, Emelianov SY. Internal Displacement and Strain Imaging Using Ultrasonic Speckle Tracking. IEEE Trans.Ultrason.Ferroelec.Freq.Contr IEEE Transactions on Ultrasonics, Ferroelectronics and Frequency Control. 1994;41(3):314–25. [Google Scholar]
- Oberai AA, Gokhale NH, Feijoo GR. Solution of Inverse Problems in Elasticity Imaging Using the Adjoint Method. inverse problems. 2003;19:297–313. [Google Scholar]
- Oberai AA, Gokhale NH, Goenezen S, Barbone PE, Hall TJ, Sommer AM, Jiang JF. Linear and nonlinear elasticity imaging of soft tissue in vivo: demonstration of feasibility. Phys Med Biol. 2009;54:1191–207. doi: 10.1088/0031-9155/54/5/006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oliphant TE, Manduca A, Ehman RL, Greenleaf JF. Complex-valued stiffness reconstruction for magnetic resonance elastography by algebraic inversion of the differential equation. Magn Reson Med. 2001;45:299–310. doi: 10.1002/1522-2594(200102)45:2<299::aid-mrm1039>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- Ophir J, Alam SK, Garra B, Kallel F, Konofagou E, Krouskop T, Varghese T. Elastography: ultrasonic estimation and imaging of the elastic properties of tissues. Proc Inst Mech Eng [H] 1999;213:203–33. doi: 10.1243/0954411991534933. [DOI] [PubMed] [Google Scholar]
- Ophir J, Cespedes I, Ponnekanti H, Yazdi Y, Li X. Elastography: a quantitative method for imaging the elasticity of biological tissues. Ultrason Imaging. 1991;13:111–34. doi: 10.1177/016173469101300201. [DOI] [PubMed] [Google Scholar]
- Ophir J, Garra B, Kallel F, Konofagou E, Krouskop T, Righetti R, Varghese T. Elastographic imaging. Ultrasound Med Biol. 2000;26(Suppl 1):S23–9. doi: 10.1016/s0301-5629(00)00156-3. [DOI] [PubMed] [Google Scholar]
- Ou JJ, Ong RE, Yankeelov TE, Miga MI. Evaluation of 3D modality-independent elastography for breast imaging: a simulation study. Phys Med Biol. 2008;53:147–63. doi: 10.1088/0031-9155/53/1/010. [DOI] [PubMed] [Google Scholar]
- Papazoglou S, Braun J, Hamhaber U, Sack I. Two-dimensional waveform analysis in MR elastography of skeletal muscles. Phys Med Biol. 2005;50:1313–25. doi: 10.1088/0031-9155/50/6/018. [DOI] [PubMed] [Google Scholar]
- Park E, Maniatty AM. Shear modulus reconstruction in dynamic elastography: time harmonic case. Phys Med Biol. 2006;51:3697–721. doi: 10.1088/0031-9155/51/15/007. [DOI] [PubMed] [Google Scholar]
- Parker KJ, Doyley MM, Rubens DJ. Imaging the elastic properties of tissue: the 20 year perspective. Phys Med Biol. 2011;56:R1–R29. doi: 10.1088/0031-9155/56/1/R01. [DOI] [PubMed] [Google Scholar]
- Parker KJ, Huang SR, Musulin RA, Lerner RM. Tissue-response to mechanical vibrations for sonoelasticity imaging. Ultrasound in Med.& Biol. 1990;16:241–6. doi: 10.1016/0301-5629(90)90003-u. [DOI] [PubMed] [Google Scholar]
- Paulsen KD, Meaney PM, Gilman LC. Alternative breast imaging: four model-based approaches. 2005. p. 253.
- Perrinez PR, Kennedy FE, Van Houten EEW, Weaver JB, Paulsen KD. Modeling of Soft Poroelastic Tissue in Time-Harmonic MR Elastography. Ieee Transactions on Biomedical Engineering. 2009;56:598–608. doi: 10.1109/TBME.2008.2009928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perrinez PR, Kennedy FE, Van Houten EEW, Weaver JB, Paulsen KD. Magnetic Resonance Poroelastography: An Algorithm for Estimating the Mechanical Properties of Fluid-Saturated Soft Tissues. Ieee Transactions on Medical Imaging. 2010;29:746–55. doi: 10.1109/TMI.2009.2035309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perreard IM, Pattison AJ, Doyley M, McGarry MD, Barani Z, Van Houten EE, Weaver JB, Paulsen KD. Effects of frequency- and direction-dependent elastic materials on linearly elastic MRE image reconstructions. Phys Med Biol. 2010;55:6801–15. doi: 10.1088/0031-9155/55/22/013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinheiro LV, Fortes CJ, Fernandes L. FINITE ELEMENT MESH GENERATOR: GMALHA. Revista Internacional De Metodos Numericos Para Calculo Y Diseno En Ingenieria. 2008;24:369–91. [Google Scholar]
- Plewes DB, Bishop J, Samani A, Sciarretta J. Visualization and quantification of breast cancer biomechanical properties with magnetic resonance elastography. Phys Med Biol. 2000;45:1591–610. doi: 10.1088/0031-9155/45/6/314. [DOI] [PubMed] [Google Scholar]
- Ponnekanti H, Ophir J, Cespedes I. Ultrasonic-Imaging of the Stress-Distribution in Elastic Media Due to an External Compressor. Ultrasound in Medicine and Biology. 1994;20:27–33. doi: 10.1016/0301-5629(94)90014-0. [DOI] [PubMed] [Google Scholar]
- Ponnekanti H, Ophir J, Huang Y, Cespedes I. Fundamental Mechanical Limitations on the Visualization of Elasticity Contrast in Elastography. Ultrasound in Medicine and Biology. 1995;21:533–43. doi: 10.1016/0301-5629(94)00136-2. [DOI] [PubMed] [Google Scholar]
- Qiu YP, Sridhar M, Tsou JK, Lindfors KK, Insana MF. Ultrasonic Viscoelasticity Imaging of Nonpalpable Breast Tumors: Preliminary Results. Academic Radiology. 2008;15:1526–33. doi: 10.1016/j.acra.2008.05.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raghavan KR, Yagle AE. Forward and inverse problems in elasticity imaging of soft-tissues. IEEE Transactions On Nuclear Science. 1994;41:1639–48. [Google Scholar]
- Reddy JN. An Introduction to the finite element method. McGraw-Hill,Inc; Hightstown, NJ: 1993. 08520. [Google Scholar]
- Richards M, Jing S, Doyely MM. Visualization of atherosclerotic plaque mechanical properties using model-based intravascular ultrsound elastography. J. Acous Soc Am. 2010;127:1730. [Google Scholar]
- Richards M, Doyley M. Inverstigating the impact of spatial priors on the performance of model-based IVUS elastography. Phys Med Biol. 2011 doi: 10.1088/0031-9155/56/22/014. In review. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richards MS, Barbone PE, Oberai AA. Quantitative three-dimensional elasticity imaging from quasi-static deformation: a phantom study. Phys Med Biol. 2009;54:757–79. doi: 10.1088/0031-9155/54/3/019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Righetti R, Garra BS, Mobbs LM, Kraemer-Chant CM, Ophir J, Krouskop TA. The feasibility of using poroelastographic techniques for distinguishing between normal and lymphedematous tissues in vivo. Phys Med Biol. 2007a;52:6525–41. doi: 10.1088/0031-9155/52/21/013. [DOI] [PubMed] [Google Scholar]
- Righetti R, Kallel F, Stafford RJ, Price RE, Krouskop TA, Hazle JD, Ophir J. Elastographic characterization of HIFU-induced lesions in canine livers. Ultrasound Med Biol. 1999;25:1099–113. doi: 10.1016/s0301-5629(99)00044-7. [DOI] [PubMed] [Google Scholar]
- Righetti R, Ophir J, Srinivasan S, Krouskop TA. The feasibility of using elastography for imaging the Poisson’s ratio in porous media. Ultrasound Med Biol. 2004;30:215–28. doi: 10.1016/j.ultrasmedbio.2003.10.022. [DOI] [PubMed] [Google Scholar]
- Righetti R, Righetti M, Ophir J, Krouskop TA. The feasibility of estimating and imaging the mechanical behavior of poroelastic materials using axial strain elastography. Phys Med Biol. 2007b;52:3241–59. doi: 10.1088/0031-9155/52/11/020. [DOI] [PubMed] [Google Scholar]
- Romano AJ, Shirron JJ, Bucaro JA. On the noninvasive determination of material parameters from a knowledge of elastic displacements theory and numerical simulation. IEEE Trans Ultrason Ferroelectr Freq Control. 1998;45:751–9. doi: 10.1109/58.677725. [DOI] [PubMed] [Google Scholar]
- Sack I, Beierbach B, Wuerfel J, Klatt D, Hamhaber U, Papazoglou S, Martus P, Braun J. The impact of aging and gender on brain viscoelasticity. Neuroimage. 2009;46:652–7. doi: 10.1016/j.neuroimage.2009.02.040. [DOI] [PubMed] [Google Scholar]
- Sack I, Bernarding J, Braun J. Analysis of wave patterns in MR elastography of skeletal muscle using coupled harmonic oscillator simulations. Magnetic Resonance Imaging. 2002;20:95–104. doi: 10.1016/s0730-725x(02)00474-5. [DOI] [PubMed] [Google Scholar]
- Samani A, Bishop J, Plewes DB. A constrained modulus reconstruction technique for breast cancer assessment. IEEE Trans Med Imaging. 2001;20:877–85. doi: 10.1109/42.952726. [DOI] [PubMed] [Google Scholar]
- Samani A, Zubovits J, Plewes D. Elastic moduli of normal and pathological human breast tissues: an inversion-technique-based investigation of 169 samples. Phys Med Biol. 2007;52:1565–76. doi: 10.1088/0031-9155/52/6/002. [DOI] [PubMed] [Google Scholar]
- Sarvazyan A, Rudenko O, Swanson S. Shear wave elasticity imaging: a new ultrasonic technology of medical diagnostics. Ultrasound in medicine. 1998. [DOI] [PubMed]
- Sarvazyan AP, Skovoroda AR, Emelianov SY, Fowlkes JB, Pipe JG, Adler RS, Roemer RB, Carson PL. Biophysical Bases of Elasticity Imaging. Acoustical Imaging. 1995;21:223–40. [Google Scholar]
- Schmitt C, Henni AH, Cloutier G. ULTRASOUND DYNAMIC MICRO-ELASTOGRAPHY APPLIED TO THE VISCOELASTIC CHARACTERIZATION OF SOFT TISSUES AND ARTERIAL WALLS. Ultrasound in Medicine and Biology. 2010;36:1492–503. doi: 10.1016/j.ultrasmedbio.2010.06.007. [DOI] [PubMed] [Google Scholar]
- Schmitt C, Soulez G, Maurice RL, Giroux MF, Cloutier G. Noninvasive vascular elastography: Toward a complementary characterization tool of atherosclerosis in carotid arteries. Ultrasound in Medicine and Biology. 2007;33:1841–58. doi: 10.1016/j.ultrasmedbio.2007.05.020. [DOI] [PubMed] [Google Scholar]
- Sinkus R, Lorenzen J, Schrader D, Lorenzen M, Dargatz M, Holz D. High-resolution tensor MR elastography for breast tumour detection. Phys Med Biol. 2000;45:1649–64. doi: 10.1088/0031-9155/45/6/317. [DOI] [PubMed] [Google Scholar]
- Sinkus R, Tanter M, Catheline S, Lorenzen J, Kuhl C, Sondermann E, Fink M. Imaging anisotropic and viscous properties of breast tissue by magnetic resonance-elastography. Magnetic Resonance in Medicine. 2005a;53:372–87. doi: 10.1002/mrm.20355. [DOI] [PubMed] [Google Scholar]
- Sinkus R, Tanter M, Xydeas T, Catheline S, Bercoff J, Fink M. Viscoelastic shear properties of in vivo breast lesions measured by MR elastography. Magnetic Resonance Imaging. 2005b;23:159–65. doi: 10.1016/j.mri.2004.11.060. [DOI] [PubMed] [Google Scholar]
- Skovoroda AR, Aglyamov SR. On reconstruction of elastic properties of soft biological tissues exposed to low-frequencies. Biofizika. 1995;40:1329–34. [PubMed] [Google Scholar]
- Skovoroda AR, Emelianov SY, O’Donnell M. Tissue elasticity reconstruction based on ultrasonic displacement and strain images. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. 1995;42:747–65. [Google Scholar]
- Skovoroda AR, Lubinski MA, Emelianov SY, O’Donnell M. Reconstructive elasticity imaging for large deformations. Ieee Transactions on Ultrasonics Ferroelectrics and Frequency Control. 1999;46:523–35. doi: 10.1109/58.764839. [DOI] [PubMed] [Google Scholar]
- Souchon R, Salomir R, Beuf O, Milot L, Grenier D, Lyonnet D, Chapelon JY, Rouviere O. Transient MR elastography (t-MRE) using ultrasound radiation force: theory, safety, and initial experiments in vitro. Magn Reson Med. 2008;60:871–81. doi: 10.1002/mrm.21718. [DOI] [PubMed] [Google Scholar]
- Sridhar M, Liu J, Insana MF. Elasticity imaging of polymeric media. Journal of Biomechanical Engineering-Transactions of the Asme. 2007a;129:259–72. doi: 10.1115/1.2540804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sridhar M, Liu J, Insana MF. Viscoelasticity imaging using ultrasound: parameters and error analysis. Phys Med Biol. 2007b;52:2425–43. doi: 10.1088/0031-9155/52/9/007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sumi C. Spatially variant regularization for tissue strain measurement and shear modulus reconstruction. Journal of Medical Ultrasonics. 2007;34:125–31. doi: 10.1007/s10396-007-0147-x. [DOI] [PubMed] [Google Scholar]
- Sumi C, Nakayama K. A robust numerical solution to reconstruct a globally relative shear modulus distribution from strain measurements. Ieee Transactions On Medical Imaging. 1998;17:419–28. doi: 10.1109/42.712131. [DOI] [PubMed] [Google Scholar]
- Sumi C, Suzuki A, Nakayama K. Estimation of shear modulus distribution in soft-tissue from strain distribution. IEEE Transactions On Biomedical Engineering. 1995a;42:193–202. doi: 10.1109/10.341832. [DOI] [PubMed] [Google Scholar]
- Sumi C, Suzuki A, Nakayama K. Phantom experiment on estimation of shear modulus distribution in soft-tissue from ultrasonic measurement of displacement vector field. Ieice Transactions On Fundamentals Of Electronics Communications And Computer Sciences. 1995b;E78A:1655–64. [Google Scholar]
- Taber LA. Nonlinear theory of elasticity: applications in biomechanics. World Scientific Publishing Co., Pte. Ltd; Singapore: 2004. [Google Scholar]
- Timoshenko SP, Goodier JN. Theory of Elasticity. McGraw-Hill Book Company; Singapore: 1970. [Google Scholar]
- Triantafyllidis D, Labridis D. A finite-element mesh generator based on growing neural networks. Ieee Transactions On Neural Networks. 2002;13:1482–96. doi: 10.1109/TNN.2002.804223. [DOI] [PubMed] [Google Scholar]
- Uffmann K, Maderwald S, Ajaj W, Galban CG, Mateiescu S, Quick HH, Ladd ME. In vivo elasticity measurements of extremity skeletal muscle with MR elastography. Nmr in Biomedicine. 2004;17:181–90. doi: 10.1002/nbm.887. [DOI] [PubMed] [Google Scholar]
- Urban MW, Greenleaf JF. A Kramers-Kronig-based quality factor for shear wave propagation in soft tissue. Phys Med Biol. 2009;54:5919–33. doi: 10.1088/0031-9155/54/19/017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Houten EE, Doyley MM, Kennedy FE, Weaver JB, Paulsen KD. Initial in vivo experience with steady-state subzone-based MR elastography of the human breast. J Magn Reson Imaging. 2003;17:72–85. doi: 10.1002/jmri.10232. [DOI] [PubMed] [Google Scholar]
- Van Houten EE, Miga MI, Weaver JB, Kennedy FE, Paulsen KD. Three-dimensional subzone-based reconstruction algorithm for MR elastography. Magn Reson Med. 2001;45:827–37. doi: 10.1002/mrm.1111. [DOI] [PubMed] [Google Scholar]
- Van Houten EE, Paulsen KD, Miga MI, Kennedy FE, Weaver JB. An overlapping subzone technique for MR-based elastic property reconstruction. Magn Reson Med. 1999;42:779–86. doi: 10.1002/(sici)1522-2594(199910)42:4<779::aid-mrm21>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- Vappou J, Maleke C, Konofagou EE. Quantitative viscoelastic parameters measured by harmonic motion imaging. Phys Med Biol. 2009;54:3579–94. doi: 10.1088/0031-9155/54/11/020. [DOI] [PubMed] [Google Scholar]
- Varghese T, Techavipoo U, Liu W, Zagzebski JA, Chen Q, Frank G, Lee FT., Jr. Elastographic measurement of the area and volume of thermal lesions resulting from radiofrequency ablation: pathologic correlation. AJR Am J Roentgenol. 2003;181:701–7. doi: 10.2214/ajr.181.3.1810701. [DOI] [PubMed] [Google Scholar]
- Vogel C. Computationa Methods for inverse problems. Siam; Philadelphia: 2002. [Google Scholar]
- Weaver JB, Van Houten EE, Miga MI, Kennedy FE, Paulsen KD. Magnetic resonance elastography using 3D gradient echo measurements of steady-state motion. Med Phys. 2001;28:1620–8. doi: 10.1118/1.1386776. [DOI] [PubMed] [Google Scholar]
- Woodrum DA, Romano AJ, Lerman A, Pandya UH, Brosh D, Rossman PJ, Lerman LO, Ehman RL. Vascular wall elasticity measurement by magnetic resonance imaging. Magnetic Resonance in Medicine. 2006;56:593–600. doi: 10.1002/mrm.20991. [DOI] [PubMed] [Google Scholar]
- Wu JR. Tofu as a tissue-mimicking material. Ultrasound in Medicine and Biology. 2001;27:1297–300. doi: 10.1016/s0301-5629(01)00424-0. [DOI] [PubMed] [Google Scholar]
- Wu Z, Hoyt K, Rubens DJ, Parker KJ. Sonoelastographic imaging of interference patterns for estimation of shear velocity distribution in biomaterials. Journal of the Acoustical Society of America. 2006;120:535–45. doi: 10.1121/1.2203594. [DOI] [PubMed] [Google Scholar]
- Yamakoshi Y, Sato J, Sato T. Ultrasonic imaging of internal vibrtation of soft tissue under forced vibration. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. 1990;UFFC-17:45–53. doi: 10.1109/58.46969. [DOI] [PubMed] [Google Scholar]
- Yorkey TJ, Webster JG, Tompkins WJ. Comparing Reconstruction Algorithms for Electrical Impedence Tomography. IEEE Trans.Biomed.Eng. 1987 doi: 10.1109/tbme.1987.326032. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Hall LO, Goldgof DB, Sarkar S. A constrained genetic approach for computing material property of elastic objects. Ieee Transactions on Evolutionary Computation. 2006;10:341–57. [Google Scholar]