Abstract
The influence of structure and age on sequence learning was investigated by testing 24 young and 24 older participants for 10 sessions in an alternating serial response time task in which pattern trials alternated with random trials. Individuals encountered lag-2 or lag-3 structure, and learning was measured by the difference (in response time and accuracy) between pattern and random trials. Both ages learned lag-2 structure, but the young learned more than the older participants. Only the young people learned lag-3 structure, and they did so more slowly and to a lesser degree than they learned lag-2 structure. These age deficits in higher order sequence learning after extended practice are consistent with simultaneity theory and with theories positing that age-related deficits in neuromodulation lead to less distinctive representations.
Implicit learning occurs when people become sensitive to covariations in the environment without intending to do so and without becoming aware of what they have learned (e.g., Cleeremans, Destrebecqz, & Boyer, 1998). Despite burgeoning interest in implicit learning over the past decade, there has been relatively little research on its aging (for a review see Prull, Gabrieli, & Bunge, 2000).
Here we focus on the perceptual–motor learning of sequences (i.e., on becoming sensitive to sequential dependencies among events). This sort of learning is involved in adapting to the routines and characteristics of new environments and acquaintances. It is important for learning languages, for learning to operate appliances, musical instruments, and computer software, and for relearning how to walk, reach, and speak after brain injury.
The small literature on the aging of sequence learning suggests that the complexity of the sequence structure influences the degree to which it can be learned by young people and the extent to which sequence learning is impaired with aging. The current study tests this hypothesis by giving people extensive training on sequences containing two different levels of structure.
The Alternating Serial Response Time Task
We use a variation of the serial response time (SRT) task developed by Nissen (e.g., Nissen & Bullemer, 1987), in which people encounter an array of four positions on a screen, each with a designated response key. On each trial, one position is filled in and the person pushes the corresponding key as quickly as possible. Typically, although the participants are not informed of this, the stimuli follow some predictable pattern (e.g., a repeating 10-element-long sequence). Learning is inferred from the fact that people come to respond faster or more accurately on blocks when the sequence follows this pattern than on blocks when the sequence is random. Salthouse, McGuthry, and Hambrick (1999) have shown that the SRT task is particularly appropriate for studying aging in that it was the only one of the implicit learning tasks they examined that showed acceptable reliability (r = .74) for individual participants.
The variation used here is the alternating SRT (ASRT) task, introduced in J. H. Howard and , in which the stimuli follow a predictable four-element-long repeating sequence. However, randomly determined stimuli alternate with these predictable stimuli. For example, if a person receives the pattern 4231, in which 1 stands for the leftmost position and 4 for the rightmost position, then the sequence encountered would be 4r2r3r1r4r2r3r1r. . ., where r stands for a randomly chosen position of the four. Thus, the predictable pattern stimuli alternate with randomly determined stimuli. In the current study, people encounter either lag-2 patterns such as the previous example, in which one random element occurs between the pattern elements, or lag-3 patterns, in which two random elements intervene (e.g., 4rr2rr3rr1rr4rr2rr3rr1rr). At any point, the amount of pattern learning can be measured by comparing performance (response time [RT] or accuracy) on pattern versus random trials. The larger this trial-type effect, the more evidence there is of pattern learning.
Theoretical Accounts of Implicit Learning
The mechanisms and neural substrates underlying implicit learning are not fully understood, but most evidence suggests that it consists of the involuntary acquisition of statistical knowledge about environmental regularities (Cleeremans & Jimenez, 1998). Such knowledge is acquired by comparing the active representation of successive events within working memory for coincidence (i.e., does an event or a series of events predict subsequent events?). This knowledge accrues gradually with experience, absorbed as if by a “structural sponge” (Hoyer & Lincourt, 1998). Implicit learning is automatic in that it occurs involuntarily, even in the absence of intent to learn. However, it does call on processing resources in that it is assumed that items must be simultaneously activated in memory in order for these regularities to be learned. Some dual-task studies support this assumption (Shanks & Channon, 2002).
Influence of Sequence Structure
Sequences differ in the structure they contain, and this structure influences learning. Two dimensions of variation have been studied. First, sequences may be either deterministic or probabilistic. Deterministic sequences are those in which elements in the pattern are completely predictable (i.e., with certainty) from one or more earlier elements. The original studies of Nissen and Bullemer (1987), for example, used a deterministic sequence of 10 repeating elements. In contrast, probabilistic sequences contain some uncertainty either by selecting events probabilistically or by occasionally inserting improbable, ungrammatical events (e.g., Cleeremans & Jimenez, 1998; Cleeremans & McClelland, 1991; Schvaneveldt & Gomez, 1998).
The structure of the ASRT sequences used here is best viewed as probabilistic. Of course, every other item (or every third item of the lag-3 sequence) is completely predictable, but only if the participant knows of the alternating pattern and can keep track of it. Our earlier studies indicate that people do not gain declarative knowledge of the pattern, even after practicing for more than 10,000 trials, unless they are told of its alternating nature. In the latter case, this knowledge has little effect on their performance, even for those people who manage to discover their pattern (D. V. ; J. H. Howard & ). Trial-by-trial analyses in our previous work with lag-2 patterns indicated that performance becomes increasingly sensitive to the frequency with which triplets of items occur.
A second, orthogonal means by which sequences are classified is in terms of the number of previous elements necessary to predict a given element. The ASRT sequences used here contain either lag-2 or lag-3 structure. That is, in sequences such as 4r3r2r1r, the lowest level of predictive relationship to be learned is between events that are separated by a lag of two trials (i.e., trial n − 2 predicts trial n). For example, consider a person who has been given the lag-2 pattern 1r2r3r4r . . . . There is no lag-0 structure to learn because each possible position occurs an equal number of times on both pattern and random trials. Nor is there any lag-1 structure because, for both pattern and random trials, all possible pairs of items are equally likely to occur. However, there is lag-2 structure in that, on pattern, but not on random, trials, certain triplets are more likely to occur than others (e.g., triplets beginning in 1 and ending in 2, beginning in 2 and ending in 3). Similarly, in lag-3 sequences such as 4rr3rr2rr1rr, the lowest level of predictive relationship is that between events separated by a lag of three trials (i.e., trial n − 3 predicts trial n). In addition, Remillard and Clark (2001) have distinguished between lag-2 and second-order structures in that for lag-2 structures only the n − 2 trial predicts trial n, whereas for second-order structures both of the preceding trials are predictive (e.g., trials n − 2 and n − 1 predict trial n). Remillard and Clark note that most studies have confounded these two kinds of structure, but this distinction is not central to the current study. What is critical is that both lag-2 and second-order structures require that the person learn relationships spanning at least three trials. Similarly, both lag-3 and third-order structures require learning about relationships spanning at least four trials.
Previous research with probabilistic sequences different from those used here has suggested that the most complex structure young people learn implicitly is lag-3 or third order and that, when compared with lower levels of structure in the same sequence, learning of higher order is slower and reaches a lower asymptote (Cleeremans & McClelland, 1991; Curran, 1997a; Peigneux et al., 2000; Remillard & Clark, 2001). Our earlier research with the ASRT is consistent with these findings in that young participants were able to learn lag-2 and lag-3 structure in a sequence in which the lowest level of structure is lag-2. In the current experiment, we ask whether young people are also capable of learning lag-3 structure when it is the lowest level present. That is, can young people learn lag-3 structural regularities, even when predictable events are embedded in an otherwise noisy sequence of events?
Influence of Aging
Several studies have found evidence that implicit sequence learning does not decline with healthy aging (e.g., Cherry & Stadler, 1995; Frensch & Miner, 1994; D. V. ). However, all of these used variations on the deterministic pattern from the original Nissen work. For example, one such regularity was 4231324321, which contains lag-0 structure (Position 3 occurred more often than Position 1) and lag-1 structure (the sequence 42 occurred more than 41). It appears now that the lack of age deficits might be due to this low-level structure because studies using more complex structures have revealed age-related deficits. Using the lag-2 ASRT regularity, we have shown age-related deficits in learning not only when college students are compared with people older than 65 but also when 65-to 75-year-old people are compared with yet older ones (J. H. Howard & ) and when middle-aged adults (34–45 years of age) are compared with those 46 to 53 years of age (Feeney, Howard, & Howard, 2002). Using a different higher order structure, Curran (1997a) has also found evidence of age-related deficits with an extreme age groups design.
We have previously interpreted these age-related deficits in terms of simultaneity mechanism, which states that older people have fewer events activated simultaneously than young people because of age-related slowing. Thus, older people are less sensitive to higher level structures than young people because such structures require that several items be activated simultaneously (J. H. Howard & ). More recent computational theories integrate simultaneity and other such information-processing-level accounts with neural mechanisms by postulating that deficits in neuromodulation, especially in cat-echolaminergic function, result in less distinctive neural representations and hence in deficient processing of context (e.g., Braver et al., 2001; Li, 2002). The evidence described previously that sequence learning deficits appear gradually over the adult life span rather than beginning in old age is consistent with these views because speed of processing and neuromodulation decline gradually across the adult life span (Li, 2002; Salthouse, 1996).
Our goal in the current study was to specify more fully age-related differences in the level of sequence structure that can be learned implicitly. Our earlier work with the lag-2 ASRT regularity (i.e., 1r4r3r2r . . .) showed that elderly people are able to learn lag-2 structure, but they do so more slowly and to a lesser degree than young people. Further, although college students were also sensitive to structure at or above lag-3, older people were not. We expect to replicate these findings of age deficits on lag-2 structures in the current study. The simultaneity hypothesis also leads us to predict that for the lag-3 sequences (e.g., 1rr4rr3rr2rr), which are used for the first time in the current study, young people will show learning, but elderly people will not.
Our earlier lag-2 studies had included substantial practice (six sessions containing 1,260 repetitions of the pattern), but here we extended training to 10 sessions and 2,100 pattern repetitions (16,800 trials). Simulations of neuromodulation theory (in which attenuation of catecholaminergic function is modeled by lowering the gain of processing units) yield age deficits in both the rate and asymptote of learning (Li, 2002). Thus, neuromodulation theory predicts that age deficits in sequence learning will not be overcome, even with extensive practice. Gathering so much data from each person also enabled trial-by-trial analyses to determine exactly what people were learning.
Method
Participants
There were 48 participants, 24 young and 24 old, each of whom completed 10 1- to 1.5-hr sessions.1 Half of those of each age were randomly assigned to each lag level. The young people were recruited from Georgetown University and the older participants from an advertisement in the Washington Post Health Section. No participant had been in similar studies, and all were paid for participating. Their characteristics are summarized in Table 1. The older participants were highly educated, reported high levels of health, and did not differ from the young on the Mini-Mental State Examination (Folstein, Folstein, & McHugh, 1975). Nonetheless, as is typical, the older participants performed more poorly on neuropsychological tests assessing memory and speed taken from the Wechsler Adult Intelligence Scale–III (Wechsler, 1997a) and the Wechsler Memory Scale–III (Wechsler, 1997b).
Table 1.
Characteristics of Participants
| Young (n = 13 F, 11 M)
|
Old (n = 13 F, 11 M)
|
|||||
|---|---|---|---|---|---|---|
| Characteristic | M | SD | M | SD | ||
| Age** (years) | 19.83 | 0.96 | 70.96 | 5.00 | ||
| Education** (years) | 13.87 | 0.54 | 16.67 | 2.66 | ||
| Self-rated healtha* | 4.54 | 0.66 | 4.04 | 0.96 | ||
| Mini-Mental State Examination | 29.67 | 0.78 | 29.12 | 1.05 | ||
| WAIS–III Vocabulary** | 52.17 | 6.87 | 45.67 | 12.05 | ||
| WAIS–III Digit Symbol** | 85.83 | 12.59 | 58.79 | 13.29 | ||
| WMS–III Letter Number Sequencing** | 13.54 | 2.26 | 9.58 | 2.32 | ||
| WMS–III Digit Span** | 22.50 | 3.86 | 17.54 | 4.00 | ||
| WMS–III Spatial Span** | 17.83 | 2.91 | 12.12 | 4.06 | ||
| WMS–III Logical Memory I Recall** | 53.08 | 6.55 | 42.25 | 8.32 | ||
Note. F = female; M = male; WAIS–III = Wechsler Adult Intelligence Scale—Third Edition; WMS–III = Wechsler Memory Scale—Third Edition.
1 = poor, 5 = excellent.
p < .05.
p < .01.
Design
The design was a 2 (age) × 2 (structure) × 2 (trial type) × 10 (session) mixed factorial, with age (young vs. old) and structure (lag-2 vs. lag-3) varying between subjects and trial type (Pattern vs. Random) and session (1–10) varying within subjects.
Procedure
Participants first completed a consent form, which had been approved by the Georgetown University Institutional Review Board, and a brief biographical questionnaire. They then completed 21 blocks of the ASRT task. At the end of the final ASRT block, they completed four blocks of the free-generation (described later). Finally, they completed a written end-of-session questionnaire containing general questions about their strategies but not referring to any regularity. Participants returned for nine additional sessions. There were no fewer than 45 min and no more than 2 days between sessions and no more than two sessions per day (except for 2 participants who had to complete three sessions in 1 day because of scheduling problems). After the free-generation task on Sessions 2 through 9, people completed one or more of the supplemental tasks listed in Table 1. Then, on the 10th and final session, after the free-generation task, participants were given a postexperimental interview described in J. H. Howard and Howard (1997, p. 637).
The ASRT task
Participants performed the ASRT task at a Macintosh computer with a 15-in. monitor. They rested their index and middle fingers on the response keys D, F, J, and K, marked with red stickers. Four open circles were evenly spaced across the middle of the screen, aligned approximately with the response keys. On each trial, one of the circles filled in with blue and remained so until the participant pushed the corresponding key. In the event of an incorrect response, this target remained until the correct key was pressed. After a 120-ms delay, the next target appeared.
People were not informed of any regularity in the events. They were instructed to press the key under the target circle as quickly as possible while maintaining an accuracy level of approximately 92%. After each block, the screen displayed their speed and accuracy for the most recent two blocks so that they could monitor their own performance. If the participant had scored less than 86% or more than 96% on both of the two most recent blocks, the experimenter reminded the participant to aim for 92% accuracy.
The following six patterns were used, with each occurring for 2 people in each Age × Structure group: 1234, 1243, 1324, 1342, 1423, 1432. Here, the numbers 1 to 4 correspond, respectively, to the positions from left to right on the screen. Each ASRT session contained 21 blocks, and each block was followed by at least a 30-s break. Each block began with 10 random trials, which were followed by enough trials for 10 repetitions of the pattern (i.e., 80 additional trials for the lag-2 groups and 120 additional trials for the lag-3 groups). Thus, each person experienced exactly 210 pattern cycles per session.
Free-generation task
The same response keys and stimulus display were used as for the ASRT. People were told to “create a sequence like the ones to which you have been responding” by pressing the keys. The keypress caused the corresponding circle to fill in. There was no feedback as to accuracy, so that no further learning of the pattern could occur. Each block consisted of either 80 (lag-2) or 120 (lag-3) responses.
Results and Discussion
Do People Reveal Declarative Knowledge of the Regularity?
Questionnaire responses were similar across ages and pattern structure and were consistent with those from earlier ASRT studies. When asked whether they noticed “any regularity in the way the stimulus was moving on the screen,” 58% answered “yes,” and almost everyone reported that they had searched for a pattern at some time during the experiment. Nonetheless, no one believed they had found the pattern; some people concluded that none was there, and others concluded that there must have been a pattern that was too subtle for them to pick up.
When at the end of the last session we told them that there was a regularity and asked them to describe anything about it that they could, most offered vague hypotheses with little confidence. The two most accurate descriptions came from people who received the lag-2 pattern 1r2r4r3r. The better of these was from a 73-year-old, who reported that “3– 4 –1 is often, but can’t predict it.” This report is correct in that such triplets (and, in fact, any 3-x-1 sequence) are among the more frequent, structure-consistent triplets. The next most accurate report was from an 18-year-old, who said the targets “moved from left to right; each finger struck the same amount of keys.” This is substantially correct in that all the targets do occur equally often, and this sequence might be construed as moving generally from left to right, although, of course, random elements intervene and the 4r3 part of the sequence violates this regularity.
Otherwise, the guesses and descriptions offered were incorrect. The most frequent were that some positions occurred more often than others, that positions on one side occurred more often than those on the other, that certain pairs of items repeated more frequently, and that doubles or triples of the same items were common.
Although people were unable to describe the regularity, many did seem aware that they were learning something, perhaps unconsciously, and many reported that this learning involved their fingers or muscles and that it led to errors. For example, 33%, distributed approximately equally across the four groups, referred to “automatic” learning and responding, “fingers” or “muscles” taking over, “unconscious” learning, or “errors” caused by such learning. For example, a lag-2 20-year-old reported, “My fingers moved automatically. I thought I knew what was going to come next. I thought my mind was subconsciously telling my fingers where to move.” A lag-3 22-year-old reported, “Sometimes I got in a rhythm and it seemed that I was not consciously aware, but that it was automatic.” According to a lag-2 66-year-old, “I couldn’t do the patterns, but I think my brain is recognizing these sequences, the part I’m not conscious of. Like riding a bicycle. Sometimes I seemed to know which direction to go.” A lag-2 80-year-old said, “It threw me off because I would want to hit a certain key, but it tricked me a lot. It made me make mistakes.” A lag-2 67-year-old commented on the “muscle memory” he was using, comparing it with how dancers move habitually because of practice.
Thus, people revealed virtually no ability to describe the regularities to which they had been exposed for 10 sessions for a total of 2,100 repetitions. Nonetheless, they did have some insight; the majority believed that some regularity was present and that it was influencing their performance in ways they could not control. We conclude, therefore, that the learning reported later is relatively pure implicit learning in that the participants revealed no declarative knowledge of the structures.
Data Reduction
The data from the 10 random trials that began each block were discarded. For the remaining trials (80 for lag-2 and 120 for lag-3), the median RT for correct trials was calculated separately for random and pattern trials for each block. Then the means of these medians were calculated across the 21 blocks in each session to yield the mean RT for each trial type for each person. Similar procedures were used for accuracy. An alpha level of .05 was used throughout, and significance tests were always two-tailed. Effect sizes reported are always for the age difference in the overall learning score, usually the trial-type effect, across all sessions combined.
Initial ASRT Analyses: Overall Accuracy and RTs
Figures 1 and 2, respectively, show RTs and accuracy across sessions for all four groups for pattern and random trials. The two most prominent features in Figure 1 are that RTs decrease over sessions and that older people respond more slowly than younger. The main effects of session, F(9, 396) = 198.08, MSE = 842.45, and age, F(1, 44) = 182.43, MSE = 32,144.87, were both significant. This change across sessions, indicating overall skill learning, is greater for the older than the younger groups, reflected in a significant Age × Session interaction, F(9, 396) = 21.27, MSE = 842.45.
Figure 1.

Mean of median response times (RTs, in milliseconds) for correct responses as a function of session, age, level of structure, and trial type. Error bars of 1 SE are visible only when larger than the symbol. Y = young; O = old; 2 = lag-2 structure; 3 = lag-3 structure.
Figure 2.

Mean proportion (Prop) correct as a function of session, age, level of structure, and trial type. Error bars of 1 SE are visible only when larger than the symbol. Y = young; O = old; 2 = lag-2 structure; 3 = lag-3 structure.
More important for assessing pattern learning (although hard to see in Figure 1), random trials are slower overall than pattern trials, and this trial-type effect increases across sessions; the main effect of trial type, F(1, 44) = 200.52, MSE = 102.20, and the Trial Type × Session interaction, F(9, 396) = 259.20, MSE = 12.49, are both significant. Most important, the magnitude of this trial-type effect varies with age and with structure. For example, the Trial Type × Age × Structure, F(1, 44) = 7.14, MSE = 102.20, Trial Type × Session × Structure, F(9, 396) = 13.12, MSE = 12.49, and Trial Type × Session × Age, F (9, 396) = 2.47, MSE = 12.49, interactions are all significant. The nature of these interactions is examined in more detail later.
For accuracy in Figure 2, it is notable that for all groups accuracy is high and constant across sessions for the pattern trials but declines for the random trials. The main effects of session, F(9, 396) = 11.54, MSE =.0004, and trial type, F(1, 44) = 288.45, MSE =.001, and the Session × Trial Type interaction, F(9, 396) = 29.97, MSE = .0001, are all significant. Probabilistic regularities, unlike deterministic ones, usually yield such increasing errors with practice (Curran, 1997a; Feeney et al., 2002; D. V. ; J. H. Howard & ; Schvaneveldt & Gomez, 1998). Participants often report that their fingers seem to take over and lead them to make more “oops” errors. Of course, unbeknownst to the participants, these errors are occurring predominantly on random trials (even though these are slower than pattern trials) and hence reflect learning of the regularity. Thus, when probabilistic sequences are used, errors become as sensitive to learning as are RTs. Figure 2 shows that older adults are more accurate than younger people, but this age difference is primarily due to the random trials. The main effect of age, F(1, 44) = 68.38, MSE = .01, and the Age × Trial Type interaction, F(1, 44) = 88.91, MSE = .001, are significant. Finally, as with RTs, the magnitude of the accuracy trial type effect varies with both age and structure; the four-way interaction of Age × Structure × Trial Type × Session is significant, F(9, 396) = 2.83, MSE =.0001.
We now examine the nature of these interactions by focusing on the questions the current study aimed to answer. In particular, we consider first whether there are age differences in learning and whether both young and older people can learn lag-2 and lag-3 structure. We then ask at what point in training it is possible to detect pattern learning and age deficits therein. We next consider whether the types of errors people make are knowledge driven and equally so for both ages and examine exactly what is being learned. Finally, we ask whether learning is revealed in the conceptually driven free-generation task.
Are There Age Differences in Learning Lag-2 and Lag-3 Structure?
Figures 3 and 4 show the trial-type effect for RTs (RT on random trials minus that on pattern) and accuracy (accuracy on pattern trials minus that on random), respectively. In both cases, higher difference scores indicate greater learning, and the age differences in learning can be seen clearly.
Figure 3.

Mean response time (RT, in milliseconds) trial-type effect (i.e., proportion correct on random trials minus that on pattern trials) for the two age groups and the two structure groups over sessions. Error bars of 1 SE are shown. Y = young; O = old; 2 = lag-2 structure; 3 = lag-3 structure.
Figure 4.

Mean accuracy trial-type effect (i.e., proportion correct on pattern trials minus that on random trials) for the two age groups and the two structure groups over sessions. Error bars of 1 SE are shown. Y = young; O = old; 2 = lag-2 structure; 3 = lag-3 structure.
The data from the lag-2 patterns replicate our earlier findings of age-related deficits (e.g., J. H. Howard & ) and indicate that the deficit remains even after 10 training sessions. The lag-2 groups revealed significant Age × Trial Type × Session interactions, F(9, 198) = 2.21, MSE = 15.06, and F(9, 198) = 7.57, MSE = .0001, for RT and accuracy, respectively. For the age difference in learning, reffect = .50 for RT and .86 for accuracy.
There are also age-related deficits in learning lag-3 patterns, although they are smaller than for lag-2, likely because the lag-3 trial type effects are small even for the young group. When the lag-3 data are analyzed alone, the Trial Type × Age, F(1, 22) = 37.00, MSE = .0001, and Age × Trial Type × Session, F(1, 22) = 2.71, MSE = .0001, interactions are both significant for accuracy, although neither is significant for RT. For the age difference in learning, reffect = .79 for accuracy and .12 for RT.
Because there was an overall age difference in accuracy, we also compared the groups using a learning measure that normalizes for overall accuracy. For each block, we divided the number of errors each person made on random trials by that person’s total number of errors. This measure revealed the same group differences as the nonnormalized accuracy data in Figure 4. For these proportional trial type effects, there are significant interactions of Age × Session, F(9, 396) = 2.78, MSE = .002, and Age × Structure, F(1,44) = 12.10, MSE = .009. For the age difference in learning, reffect = .80 for lag-2, and .35 for lag-3.
Thus, we conclude that there are age differences in sensitivity to repeating regularities in the environment for both lag-2 and lag-3 structures and that these age effects can be detected by accuracy or RT trial-type effects (for pattern vs. random trials) and by normalized proportions of errors occurring on random trials.
Can Participants of Both Ages Learn Lag-2 and Lag-3 Structure?
To find out, we performed Trial Type × Session ANOVAs for each of the four groups separately. In keeping with the unambiguous evidence of pattern learning for the young and old lag-2 groups and for the young lag-3 group in Figures 3 and 4, there are significant Trial Type × Session interactions for all three of these groups for both accuracy and RT. The least significant of these comparisons was that for the young lag-3 group’s RT data, in which F(9, 99) = 2.90, MSE = 4.50. Whether older people can learn lag-3 patterns is less clear. Although Figures 3 and 4 show this group’s trial-type effect hovering slightly above zero throughout training for both measures, there is no noticeable increase beyond Session 1. In keeping with this observation, the older lag-3 group’s Trial Type × Session interaction was not significant for either measure ( p > .80), even though they do reveal a significant trial-type effect for both RT, F(1, 11) = 10.23, MSE = 53.38, and accuracy, F(1, 11) = 12.30, MSE = .0001. The quadruplet analyses described in a later section help to clarify why this small, constant trial-type effect is occurring for the older lag-3 group.
So far, then, we conclude that young people can learn both lag-2 and lag-3 structures, even when there is no lower level structure in the sequence. However, more exposure is needed for lag-3 than for lag-2 structure, and lag-3 learning is revealed primarily by accuracy. This finding that young people are able to learn lag-3 regularities is consistent with the work of Cleeremans and McClelland (1991) and Remillard and Clark (2001), but the sequences in these earlier studies had also contained lower level structure. Thus, the current finding demonstrates that young people can learn lag-3 structure even when no lower level structure is present. We find that older people are able to learn lag-2 regularities, but they show little, if any, learning of lag-3 structure when that is the lowest level of structure present.
How Early in Training Can Pattern Learning and Age Deficits Be Detected?
We examined the onset of learning by dividing each of the first two sessions into four epochs, with the first three epochs of each session containing five blocks (i.e., 50 repetitions of the pattern) and the last containing six blocks. The mean RT and accuracy for these first eight epochs for both age groups are shown in Figure 5 for the lag-2 structure and in Figure 6 for the lag-3 structure.
Figure 5.

For lag-2 structures, mean of median response times (RTs, in milliseconds) for correct responses (top) and mean proportion (Prop) correct (bottom) for the first two sessions only as a function of epoch, age, and trial type. Error bars of 1 SE are visible only when larger than the symbol. P = pattern trials; R = random trials.
Figure 6.

For lag-3 structures, mean of median response times (RTs, in milliseconds) for correct responses (top) and mean proportion (Prop) correct (bottom) for the first two sessions only as a function of epoch, age, and trial type. Error bars of 1 SE are visible only when larger than the symbol. P = pattern trials; R = random trials.
Figure 5 suggests, and ANOVA confirms, that lag-2 RTs show significant evidence of pattern learning but not an age difference therein; the Epoch × Trial Type interaction is significant, F(7, 154) = 5.63, MSE = 52.92, but no Trial Type × Age interactions approach significance. For the age effect on learning, reffect = .10. The t tests indicate that both age groups first show a significant RT trial type effect on Epoch 5, t(11) = 2.80 and 5.48, for young and old, respectively.
The accuracy data for the lag-2 groups in Figure 5 indicate that both ages show learning, but the young do so earlier. There were interactions of Epoch × Trial Type, F(7, 154) = 7.49, MSE = 4.59E-4, and Age × Trial Type, F(1,22) = 32.14, MSE = .001, reffect = .77. The young group first showed a significant trial type effect on Epoch 1, t(11) = 2.94, whereas the old group first did so on Epoch 4, t(11) = 2.37. Thus, both ages showed learning on accuracy before RTs. On accuracy, the young group revealed significant learning within the first 50 repetitions of the pattern, whereas the older group did not do so until between 150 and 210 repetitions. The age groups differ significantly from each other on this accuracy trial type effect as early as the second epoch, t(22) = 2.80 (i.e., within the first 100 pattern repetitions).
The lag-3 data in Figure 6 show smaller and more variable learning effects. RTs reveal no significant effects of trial type at all during the first two sessions. Accuracy does yield significant effects of trial type, F(1, 22) = 30.66, MSE = 2.69E–4, and Trial Type × Age, F(1, 22) = 7.92, MSE = 2.69E–4. For the age difference in learning, reffect = .23 for RT and .50 for accuracy. When examined alone, the young group reveals a significant accuracy trial-type effect, F(1, 11) = 40.80, MSE = 2.31E–4, but the older group does not. Thus, there is evidence of lag-3 learning within the first two sessions for the young people but not the older people.
In summary, analyses of the first two sessions indicate that, on accuracy, age deficits in lag-2 learning are detectable within the first 100 repetitions of the pattern.
Are the Types of Errors Knowledge Driven and Equally So for Both Ages?
The accuracy analyses so far have focused on whether people make errors, but here we ask what kind of errors people make. One way of accounting for overall performance on this task is to assume that as people gain experience with the sequences, they build up a model of the regularity. This model primes items that are likely in context. As this model grows more accurate, it primes correct responses on pattern trials, but it will often prime incorrect responses on random trials, thus leading accuracy and RT on random trials to diverge from pattern trials. This interpretation suggests that when people do make errors on random trials, those errors should be structure consistent and increasingly so as they learn the regularity.
We examined all the random trials on which each person made an error and classified them as either structure consistent or structure inconsistent. For lag-2 patterns, a structure-consistent error results in a triplet that could occur on pattern trials, whereas a structure-inconsistent error does not. For example, if a participant whose pattern was 1r2r3r4r encountered the sequence 144, then incorrectly responding to the last item in the triplet with a 2 would be considered a structure-consistent error, whereas incorrectly responding with a 3 would be considered a structure-inconsistent error. For each person, we determined the percentage of all errors on random trials that were structure consistent. We did a similar count for the lag-3 pattern using quadruplets. The mean proportions for all four groups are shown in Figure 7.
Figure 7.

Mean proportion (Prop) of structure-consistent errors produced on random trials as a function of session for both ages and structures. Error bars of 1 SE are shown. 2 = lag-2 structure; 3 = lag-3 structure.
Figure 7 suggests, and ANOVA confirms, that a greater proportion of the errors are structure consistent for the lag-2 than for the lag-3 patterns, F(1, 44) = 126.49, MSE = .01, and for the younger than older people, F(1, 44) = 108.73, MSE = .01. For the age difference in learning, reffect = .89 for lag-2 and .75 for lag-3. In addition, the proportion of structure-consistent errors increases significantly over sessions for the young people for both lag-2 and lag-3 patterns but does not increase for the older groups. This Age × Session interaction is significant, F(9, 396) = 2.42, MSE = .003. Subsequent one-way ANOVAs for each of the four groups revealed significant session effects for the young lag-2, F(9, 99) = 2.23, MSE = .004, and young lag-3 groups, F(9, 99) = 3.22, MSE = .001, but not for the two older groups ( p > .15).
The young people were different from chance (i.e., .25)2 on every session in both the lag-2 and lag-3 groups, ts(11) = 2.79–13.17. For the older lag-2 group, this proportion was different from chance ( p > .05) on all sessions except Sessions 3 and 7, but the older lag-3 group differed from chance only on Sessions 5 and 8.
These findings indicate a notable difference in the kinds of errors, with the younger people making knowledge-driven errors for both lag-2 and lag-3 patterns and increasingly so as they gain experience. The older people make fewer knowledge-driven errors, and their proportion does not increase with experience.
What Is Being Learned and Are There Age Differences Therein?
As experimenters, we know that there is an alternating regularity that makes certain trials completely predictable, but people who show trial-type effects are not necessarily learning this. In fact, no one reported awareness of such a structure.
Lag-2 structure
When the lag-2 groups show a trial-type effect, the lowest level of regularity they could be learning is that some triplets occur more frequently than others. For example, if a person’s pattern is 1r2r3r4r, then triplets beginning with 1 and ending with 2 will be more frequent than triplets beginning with 3 and ending with 2.
The fact that people are more accurate and faster on pattern than random trials indicates that they became sensitive to these differences in triplet frequency, but it does not reveal exactly what they have learned. To find out, we parsed each lag-2 person’s event sequence into a series of overlapping triplets using a sliding three-trial window. Each triplet was then sorted into one of five categories. The first category contained pattern triplets (P; i.e., those ending on a pattern trial). The remaining four triplet types ended on random trials. Random-consistent (RC) triplets are those that by chance form a structure-consistent triplet; they are identical to P triplets except that they end on a random trial. Random repetition (RR) triplets contain repetitions of a single element (e.g., 111 or 444) and random span (RS) triplets begin and end with the same element (e.g., 121 or 434), with a different middle element. The remaining triplets were classified as random inconsistent (RI); these end in a random trial and are neither structure-consistent (RC), repetitions (RR) nor span (RS) triplets.
We separated RR and RS triplets from RI triplets because of evidence that they may be distinct from other triplet types (e.g., Remillard & Clark, 2001) and because RR and RS triplets can only occur on random trials, and this is so not only for a given participant but across all participants. Thus, it is important to examine how the overall trial-type effects described previously are influenced by these RR and RS triplets.
Figure 8 shows the RTs and the accuracy data, broken down by the five triplet types for young and old lag-2 groups. Examining first the RR triplets (e.g., 222), it is clear that even though they occur rarely (overall probability of .031) people of both ages respond to them quickly and accurately. Thus, RR triplets are actually working against finding an overall trial-type effect (i.e., pattern vs. random difference) because these are random trials that are both accurate and fast, perhaps reflecting simple motor priming. In contrast, RS triplets (e.g., 121) are the slowest and least accurate triplets from the beginning for both age groups, and their accuracy declines over sessions. To examine how these triplets might have contributed to the overall trial-type effects, we conducted ANOVAs comparing RS triplets with P triplets. For RTs, there was a significant Triplet Type (P vs. RS) × Session interaction, F(9, 198) = 11.15, MSE = 58.35, but no Triplet Type × Age interaction, F(1, 22) = 1.56, MSE = 1,170.04, reffect = .26. Thus, P trials get faster than RS over sessions, reflecting learning, but to the same extent for both ages. For accuracy, in contrast, there was a Triplet Type × Session interaction, F(9, 198) = 16.98, MSE =.001, and a Triplet Type × Age × Session interaction, F(9, 198) = 3.790, MSE = .001. For the age difference, reffect = .87.
Figure 8.

For the lag-2 groups, mean of median response times (RTs, in milliseconds) for correct responses as a function of session and triplet type for the young (top left) and old (top right) and mean proportion (Prop) correct for the young (bottom left) and old (bottom right). Error bars of 1 SE are visible only when larger than the symbol. P = pattern triplets; RC = random consistent; RI = random inconsistent; RR = random repetition; RS = random span.
Thus, RS triplets are slower and less accurate than P triplets and increasingly so with practice. This is the case for both age groups but more so for the young. This suggests that part of what each age group has learned tacitly is that alternations are rare, and young people’s responses are more sensitive to this regularity than older. These RS triplets are increasing the overall trial-type effects and contributing to the overall age deficit in sequence learning.
Is the rarity of alternations all that is being learned, and is it the only source of the age deficit in learning? ANOVAs comparing P and RI triplets in Figure 8 suggest that this is not the case. Both RT, F(9, 198) = 2.33, MSE = 22.97, and accuracy, F(9, 198) = 6.40, MSE = 2.32E–4, analyses revealed significant Age × Session × Triplet Type (P–RI) interactions. For the age difference in learning, reffect = .47 for RT and .83 for accuracy.
Subsequent ANOVAs indicated that each age group alone revealed significant Session × Triplet Type interactions on both dependent measures ( p < .01 in all cases). Therefore, over sessions, people of both ages became sensitive to which triplets were most frequent, but the young were more sensitive than the old. Most important, these effects are not due simply to people learning that repetitions and alternations are rare, because RR and RS triplets have been eliminated from this analysis.
Finally, we compared P and RC triplets. If the highest level of regularity people are learning is triplet frequency, then RTs and accuracy to the last events in RC triplets should be the same as those to P triplets because the triplets are identical, differing only in whether they happened to end on a pattern or random trial. In contrast, if people are learning more than triplet frequency, then P triplets should lead to better performance than RC triplets.
The RTs in Figure 8 reveal a small P–RC separation for the younger participants by Sessions 9 and 10, whereas there is no sign of such separation for the older group. When analyzed alone, the young group shows a significant Session × Triplet Type (P vs. RC) interaction, F(9, 99) = 3.08, MSE = 19.44, whereas the old group reveals no effects of triplet type. (However, an ANOVA comparing the age groups failed to yield any significant Age × Triplet Type interactions. For the age difference in learning, .08.) For accuracy, Figure 8 suggests that both ages are reffect = showing some separation between P and RC triplets, although the effect is larger and more systematic for the younger group. The Age × Triplet Type interaction is significant for accuracy, F(1, 22) = 7.65, MSE = 4.53E–4, reffect = .48. When the young and old groups are analyzed separately, both show main effects of triplet type; for the young group, F(1, 11) = 33.77, MSE = .001, and for the old group, F(1, 11) = 8.75, MSE = 3.42E–4. The young group also yielded a significant Session × Triplet Type interaction, F(9, 99) = 2.64, p = .01, MSE = 4.07E–4, but the older group did not.
Concerning the P versus RC comparison, then, we conclude that early on, both groups are learning only that some triplets are more frequent than others and hence show no P–RC separation. However, with continued exposure to the regularity, both groups, particularly the younger, engage in some higher order learning as well. In general, these findings are consistent with our earlier work (J. H. Howard & ) in which people completed only 6 sessions, except that in that case the older groups did not reveal any consistent P–RC difference. The evidence for some higher order learning (beyond triplets) among the elderly in the current study is likely due to the more extended learning and to the greater power provided by the larger sample sizes.
To summarize, triplet analyses of the lag-2 data indicate that young and old people learn that alternations are rare (P–RS comparisons) and, beyond that, certain triplets are more frequent than others (P–RI comparisons). In addition, both ages show some evidence of higher order (beyond triplet frequency) learning with extended training (P–RC comparisons). However, all of these effects are larger and tend to appear earlier for young people than for older, and all reflect tacit knowledge in that people did not report these regularities when asked to describe their sequences.
Lag-3 structure
To determine exactly what people are learning of lag-3 structure, quadruplets, instead of triplets, were analyzed. The data for the five quadruplet types described previously are shown in Figure 9.
Figure 9.
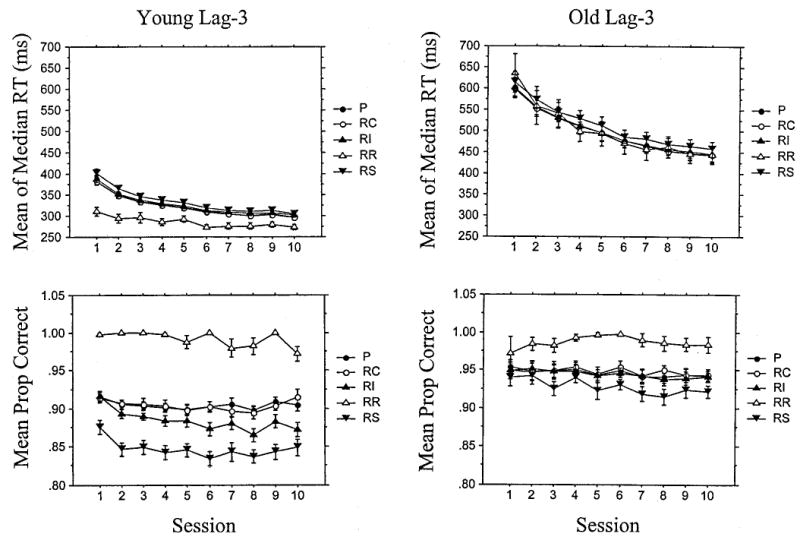
For the lag-3 groups, mean of median response times (RTs, in milliseconds) for correct responses as a function of session and triplet type for the young (top left) and old (top right) and mean proportion (Prop) correct for the young (bottom left) and old (bottom right). Error bars of 1 SE are visible only when larger than the symbol. P = pattern triplets; RC = random consistent; RI = random inconsistent; RR = random repetition; RS = random span.
The repetitions (RR) quadruplets (e.g., 4444) are highly accurate from the beginning for both age groups and very fast for the young people. As for the lag-2 patterns, this is likely due to motor priming rather than learning per se.
Figure 9 suggests that RS quadruplets (e.g., 1231, 4224), like RS triplets, are less accurate and slightly slower than other quadruplets from the beginning of training. For RTs, there was a significant Session × Quadruplet Type (P–RS) interaction when both age groups are combined, F(9, 198) = 1.95, MSE = .25.41, but no Age × Trial Type interactions were significant. For the age difference in learning, reffect = .38. Surprisingly, the P–RS difference is slightly greater on Session 1 than Session 10 (mean difference = 16 and 11 ms, respectively). Thus, the P–RS difference does not seem to reflect learning but rather a preexisting tendency in both age groups to respond relatively slowly to the RS quadruplets. Accuracy reveals a significant Session × Quadruplet Type interaction, F(9, 198) = 2.01, MSE = .1.64E–4, indicating that the accuracy difference favoring P over RS quadruplets increases over trials (although this difference is relatively small: .028 on Session 1 and .038 on Session 10). There was also an Age × Quadruplet Type interaction, F(1, 22) = 35.87, MSE = .001, reffect = .79, but no triple interaction. In the case of accuracy, the P–RS difference was greater for the young than the old groups, although both individually show significant P–RS effects ( p < .01 in both cases).
Thus, for lag-3 structures, both ages respond more slowly and less accurately to RS trials (such as 1441 or 2342) than to pattern trials. This only partly reflects learning in that these P–RS differences are present from Session 1 and increase little across sessions for accuracy and not at all for RT. Further, on accuracy, this P–RS difference is larger for young than for older people.
Is this poor performance on the RS trials the sole cause of the overall trial type effects (pattern vs. random trials) for the lag-3 groups? Visual inspection of the P versus RI quadruplets in Figure 9 suggests that it might be for the older people in that the P and RI functions are similar to each other on both measures. In contrast, Figure 9 suggests that the younger people are distinguishing between P and RI quadruplets on the accuracy measure, with these trial types diverging gradually. An ANOVA of accuracy confirms this in that there is a significant Session × Quadruplet Type (P-RI) × Age interaction, F(9, 198) = 3.29, MSE = 9.68E–5. For the age difference in learning, reffect = .83. Subsequent ANOVAs revealed a significant Session × Quadruplet Type interaction for the young group ( p < .01), but no effects of quadruplet type at all for the old group. The RT ANOVA yielded more ambiguous results in that there was an overall effect of quadruplet type when both ages were combined, F(1, 22) = 23.16, MSE = 34.70, but no significant quadruplet type interactions with age. For the age difference in learning, reffect = .13. The overall quadruplet type effect is due to a small but persistent advantage of only 3 ms for the P versus the RI trials when averaged over sessions and age groups.
Thus, for lag-3 patterns, the young people are differentiating (and increasingly so with training) between P and RI quadruplets as revealed by the accuracy measure, even when RR and RS quadruplets are removed, whereas older people are not. Thus, the quadruplet analyses suggest that younger people are sensitive to the lag-3 structure, but older people are not. The small trial-type effects the older lag-3 groups revealed in the original analyses reflect preexisting tendencies to respond less quickly and accurately to the RS quadruplets.
Finally, we examined whether people were learning higher order information beyond the relative frequencies of quadruplets by comparing P with RC quadruplets. Visual inspection of Figure 9 suggests that neither age group is doing so on either measure, and an ANOVA of the accuracy data yielded no significant effects of quadruplet type (P–RC). Surprisingly, the ANOVA of RTs did reveal a significant Age × Quadruplet Type × Session interaction, F(9, 198) = 2.43, MSE = 16.61, but this was paradoxically due to the young people responding slightly more slowly to P than RC trials during the first two sessions only. In the absence of an explanation for this reversal, we attribute it to a Type I error.
To summarize, the lag-3 data indicate that young and old people respond slowly and less accurately to RS quadruplets than to other types (P vs. RS), and this tendency is largely preexisting. In addition, younger people learn that some other quadruplets are more frequent than others (P vs. RI), but older people do not. Further, neither group learns any higher order information beyond quadruplet frequency (P vs. RC).
Is Learning Revealed in the Free-Generation Task?
People performed the free-generation task at the end of each session. To find out whether the sequences people produced showed the influence of the regularity, we divided each lag-2 person’s output into a series of triplets by stepping a three-item window through the responses, one response at a time. We then sorted each of these triplets into one of four categories, corresponding to those in the triplet analyses just discussed. Repetitions (R) were repetitions of the same three positions (e.g., 333). Spans (S) were triplets starting and ending with the same position (e.g., 313) that were not repetitions. Inconsistent (I) triplets were inconsistent with the person’s pattern (but were neither R nor S triplets). Consistent (C) triplets were those that were consistent with the person’s pattern. We normalized the total count for each triplet type by the number of unique triplets, thus obtaining the mean generation rate per triplet for each category. We analyzed the lag-3 data in the same way, except using quadruplets instead of triplets.
The ANOVAs reported later are based on all 10 sessions. However, these data were variable and changed little over sessions, so Figure 10 only shows the mean generation rates for Sessions 1 and 10. For completeness, all four triplet (quadruplet) types are shown, but the critical comparison is that between the C and I triplets, which are counterbalanced across participants, in that a given triplet is consistent for some participants and inconsistent for others. So, unlike R and S types (which might reflect preexisting tendencies), if C and I types yield different generation rates, this must be due to the specific experience people had with their assigned regularity. Therefore, it is noteworthy that C and I triplets (and quadruplets) in Figure 10 do not differ from each other for either age group or lag. ANOVAs revealed no significant main effects or interactions of triplet or quadruplet type (C vs. I). Thus, when the uninterpretable R and S types are eliminated from consideration, no group produced structure-consistent sequences during the free-generation task, and thus we find no evidence that people can use their pattern knowledge in the absence of stimuli in this conceptually driven task.
Figure 10.

Mean free-generation rate for triples (lag-2) or quadruples (lag-3) of four types for young and old people for Sessions (Sess) 1 and 10. Error bars show 1 SE. C = consistent; R = repetition; S = span; I = inconsistent (other than R and S) triplets (for lag-2) or quadruplets (for lag-3).
General Discussion
We found age-related deficits in implicit learning of a perceptual–motor sequence using an alternating version of a serial RT task in which predictable pattern events alternated with one (lag-2) or two (lag-3) randomly determined events. Young and older people learned sequences containing lag-2 structure, but the onset and asymptote of learning and the nature of the errors revealed age-related deficits. These deficits in lag-2 learning were detectable early in training and became larger with practice. Young people also learned lag-3 sequences, albeit more slowly and to a lower asymptote than lag-2, but older people showed little or no learning of the lag-3 structure.
These findings extend earlier findings in two major ways. The first concerns how structure influences learning in young people. Earlier results suggested, and those here confirm, that the highest order of structure young people learn implicitly is lag-3 or third order. Our results also confirm that lag-3 structure is learned more slowly and to a lower asymptote than lag-2 structure (Cleeremans & McClelland, 1991; Curran, 1997a; Peigneux et al., 2000; Remillard & Clark, 2001). Previous studies of lag-3 learning have used sequences that also contain lower levels of regularity (e.g., lag-2), unlike the alternating regularity used here. Therefore, our findings go beyond earlier ones in showing that young people can learn lag-3 structure from sequences lacking any lower level structure. Nonetheless, there are limits on how much young people learn about such noisy sequences. Young peoples’ trial-type effects for lag-3 sequences are smaller after 10 sessions than the trial-type effects that emerge by Session 2 for lag-2 sequences. Hence, young people learn sequential regularities even when they are embedded in an extremely noisy sequence, but there are limits on the amount of such learning, and these limits are not overcome by extended practice.
The second contribution concerns how structure influences age differences in sequence learning. Our finding that older people can learn lag-2 structure, but to a lesser degree than young people, is consistent with and our own earlier findings (D. V. ; J. H. Howard & ). The current results indicate, in addition, that older people show little, if any, learning of lag-3 structure, at least when this is the lowest level of structure present; the lag-3 elderly groups showed no consistent evidence of trial-type effects. The older lag-2 group did show some evidence of learning beyond second order on the triplet analyses (P vs. RC) when lower level structure was present. However, even there, older people showed less such higher-order learning than young people. Further, the current results indicate that these age deficits in learning lag-2 and higher structures persist even after extended practice spanning 10 sessions and more than 2,100 repetitions of the regularity. Thus, at least in perceptual–motor tasks of the sort studied here, older people are largely insensitive to regularities spanning more than three items.
Age Deficits in Learning or Only in Performance?
There are several indications that the trial-type deficits observed reflect age deficits in learning and are not just performance differences caused by the older groups’ lower overall error rates. First, in J. H. Howard and , we matched a young and an old group on overall accuracy in the ASRT task. When we did so, we still found significant age deficits in trial-type effects. Second, in the current study, we found that normalized error scores, consisting of the proportion of a person’s total errors that occurred on random trials, also revealed age deficits. Third, in the current study, when we examined the kinds of errors that people made, we found that older people’s errors were less likely than young people’s errors to be structure consistent. Thus, we conclude that older people have learned less about the regularity than younger.
Are Age Deficits Due to Implicit or Explicit Learning?
There is continuing debate as to how to differentiate empirically between implicit and explicit learning and on how to assess awareness and the presence of declarative knowledge (Shanks & St. John, 1994). It is agreed that tasks are rarely process pure. This is important for age comparisons because age deficits in explicit learning are well established (Prull et al., 2000). Thus, it might be argued that the age deficits observed here reflect age deficits in explicit learning.
Evidence suggests, however, that learning in the ASRT task is largely implicit. First, people’s verbal reports indicate that they are uniformly unable to describe the regularity, even though, if they did discover it, the alternating regularity should be easy to state in words. In addition, it is not that people are unwilling to guess. Even though their verbal reports rarely describe anything accurate about the pattern (i.e., they rarely name any triplets that were particularly frequent), they often do describe regularities that are incorrect (i.e., that repetitions of two or three items in a row are frequent).
Second, the free-generation data in the current experiment indicate that when instructed to do so, people do not generate sequences that contain details of the regularity they had encountered, even though their RT and accuracy during the ASRT task itself indicated that they were sensitive to these regularities. For example, the triplet analyses revealed that lag-2 groups of both ages responded more quickly and accurately to structure-consistent (P) events than to structure-inconsistent (RI) events during the ASRT task. Nonetheless, during the free-generation task, people were no more likely to produce pattern-consistent than pattern-inconsistent triplets. This same dissociation occurred for the lag-3 young people; their performance distinguished between the P and I quadruplets during the ASRT, but not the free-generation task.
Third, in other ASRT studies, we have included sensitive recognition and sorting tests that failed to reveal any ability to discriminate between structure-consistent and structure-inconsistent sequences (Japikse, Howard, & Howard, 2001; Negash, Howard, Japikse, & Howard, 2003). We conclude that young people learn lag-2 and lag-3 structure implicitly and that the age deficits observed are not due to explicit learning deficits.
Implications for Theory
The current findings suggest that, without awareness, people build up a mental model of the stochastic structure of the sequence (in this case, the frequencies with which triplets or quadruplets occur), perhaps by connectionist principles (Cleeremans & Jimenez, 1998). Early on in experience with a given task or environment, responding is based primarily on data-driven processes: People simply respond to the events they encounter. However, with experience, their mental model becomes richer, and knowledge-driven processes play an increasingly important role in responding. Although this enables more efficient processing of predictable events, it can also lead to increasing errors for unexpected events, which occur in probabilistic sequences such as those used here (and often in daily life; Schvaneveldt & Gomez, 1998). Thus, the smaller trial-type effects and fewer knowledge-based errors we observe for older people suggest that healthy aging is accompanied by an impaired ability to acquire a mental model of sequential structure.
What cognitive mechanisms underlie this deficit? We have appealed to Salthouse’s simultaneity mechanism of cognitive aging (Salthouse, 1996); because of cognitive slowing, older people have less information available simultaneously than do younger people and so they develop an impoverished mental model (D. V. ; J. H. Howard & ). This view attributes the age impairment to a capacity limitation: Old people are unable to keep enough of the recent past activated simultaneously to learn how it relates to present and future events.
That older people are poorer than young people at learning lag-2 structure and show little learning of lag-3 structure is consistent with this interpretation. However, it is possible that aging brings not only a reduction in capacity but also a reduced ability to form associations among activated items. This latter binding-deficit view builds on the finding that elderly people have difficulty associating two or more items or features in memory (Mitchell, Johnson, Raye, Mather, & D’Esposito, 2000; Naveh-Benjamin, 2000). Age deficits in sequence learning may reflect a more general binding impairment because sequence learning entails binding information across time.
The binding hypothesis goes beyond simultaneity in assuming that, even when older people activate two items simultaneously (which is necessary to learn lag-1 structure), they are less able than young to form an association between them. Of course, most evidence for such binding deficits comes from explicit measures of learning and memory. Whether there are age deficits in learning new associations on implicit tests of memory is still unclear (e.g., Light, Prull, LaVoie, & Healy, 2000). The fact that classical eyeblink conditioning shows age-related deficits (e.g., Woodruff-Pak & Jaeger, 1998) suggests that at least one kind of implicit learning is age sensitive, even though it requires binding only two events: the conditioned stimulus and the unconditioned stimulus.
The fact that most early studies of SRT learning revealed age constancy does not necessarily argue against a binding deficit. To our knowledge, all of the studies that have revealed age constancy in SRT learning used structures that contained some 0th-order regularity, that is, individual events differed in frequency (e.g., Cherry & Stadler, 1995; Frensch & Miner, 1994; D. V. ; Salthouse et al., 1999). Hence, the lack of age deficits could have been due to age equivalence in learning the frequency of occurrence of individual events (which presumably does not require binding) rather than in learning first- (lag-1) and higher order structure.
Both the simultaneity and the binding explanations are consistent with theories that attribute many aspects of cognitive aging to a general age-related deficit in neuromodulation (Braver et al., 2001; Li, 2002). At the biological level, age impairments are thought to reflect changes in the dopamine system as manifest in impaired dorsolateral prefrontal cortical function. These neuromodulation deficits result in healthy elderly suffering “cognitive control impairments resulting from a failure to properly represent and maintain context information” (Braver et al., 2001). One characteristic of neural networks that simulate such neuromodulation deficits is that such “aged” networks act like the elderly participants in the current study in revealing deficits in asymptotic learning even after extended practice (Li, 2002).
The neuromodulation theory can potentially integrate the simultaneity and binding accounts into a single conceptual framework that ties the behavioral findings to their neural mechanisms. In this sense, the neuromodulation framework, like the simultaneity and binding views, points to frontal lobe impairments as being central to cognitive aging. Therefore, it is important that imaging and patient studies indicate that the prefrontal cortex is involved in learning higher order sequence structure (Gomez Beldarrain, Grafman, Ruiz De Velasco, Pascual-Leone, & Garcia-Monco, 2002; Sakai et al., 1998). Of course, this does not exclude the possibility that other structures (e.g., medial temporal lobe) also contribute to age deficits; there is some evidence from amnesia patients and imaging studies for medial temporal lobe involvement in the learning of higher order sequences (Curran, 1997b; Schendan, Searl, Melrose, & Stern, 2003). Although the age deficits in the current experiment are consistent with the neuromodulation/context-deficit perspective, additional work is required to distinguish or integrate the simultaneity, binding, and neuromodulation-deficit views of age-related sequence learning impairment.
Practical Implications
In the case of implicit learning of sequences, the aged person’s glass is both half full and half empty. From the half-full perspective, the ability to learn lag-2 structure implicitly continues at least into the decade of the 80s, even though older people are often not aware that they are learning. This ability enables people to remain sensitive to subtle regularities in their environment and to thus adapt to a changing world. Such implicit learning is spared compared with more strategic kinds of learning. For example, we have found that when given intentional instructions to discover and describe the pattern in lag-2 ASRT sequences, some young people were able to do so, but no elderly people could, even though both groups showed significant implicit learning as revealed by trial-type effects (D. V. ).
On the half-empty side, higher order sequential structure is thought to be important for learning language (e.g., Conway & Christiansen, 2001) and skills such as using a software package. Thus, the age-related deficits in learning higher order sequential structure observed here probably make it more difficult for older people to acquire new skills and less likely that they will become sensitive to subtle regularities in their environment, even after extended exposure.
Establishing what levels and kinds of implicit learning are impaired and what factors affect such learning should be useful for designing environments and educational programs that take advantage of the older person’s spared capacities and compensate for those that have declined.
Acknowledgments
We thank Laura Romain for assistance with data coding and Nancy Dennis, Cherie Marvel, Selam Negash, Barbara Schwartz, Chandan Vaidya, and Helen Yankovich for comments. We thank Luis Jiminez for suggestions on the manuscript.
Footnotes
A preliminary report of these findings was presented at the Cognitive Aging Conference, Atlanta, GA, April 2000.
This research was supported by National Institute on Aging Grant R37AG15450 and by National Institute on Deafness and Other Communication Disorders Predoctoral Fellowship DC00296.
Data from 6 additional people were discarded. One young and 1 old person had to drop out because of scheduling difficulties. One old person reported at the end of the 10 sessions that she had used different fingers on different blocks, and 3 older persons were discovered to have participated in an earlier similar experiment after testing was completed.
To determine chance, for the lag-2 structure, consider what occurs for each set of four triplets (e.g., 111, 112, 113, and 114). There is always one consistent and three inconsistent triplets. For all inconsistent triplets, the probability of producing a structure-consistent error is .33 (i.e., one out of the three possible errors is structure consistent). For the consistent triplet, however, the probability of producing a structure-consistent error is 0 because all the errors would be structure inconsistent). So the overall probability of producing a structure-consistent error over this set of four triplets is as follows: ([.33*3] + [0*1])/4 = .25. This can be generalized to the whole set of triplets, where the same structure is repeated 16 times. Similar considerations for the lag-3 structure yield the same .25 value for chance.
References
- Braver TS, Barch DM, Keys BA, Carter CS, Cohen JD, Kaye JA, et al. Context processing in older adults: Evidence for a theory relating cognitive control to neurobiology in healthy aging. Journal of Expermental Psychology: General. 2001;130:746–763. [PubMed] [Google Scholar]
- Cherry KE, Stadler MA. Implicit learning of a nonverbal sequence in younger and older adults. Psychology and Aging. 1995;10:379–394. doi: 10.1037//0882-7974.10.3.379. [DOI] [PubMed] [Google Scholar]
- Cleeremans A, Destrebecqz A, Boyer M. Implicit learning: News from the front. Trends in Cognitive Sciences. 1998;2:406–416. doi: 10.1016/s1364-6613(98)01232-7. [DOI] [PubMed] [Google Scholar]
- Cleeremans, A., & Jimenez, L. (1998). Implicit sequence learning: The truth is in the details. In M. A. Stadler & P. A. Frensch (Eds.), Handbook of implicit learning (pp. 323–364). Thousand Oaks, CA: Sage.
- Cleeremans A, McClelland JL. Learning the structure of event sequences. Journal of Experimental Psychology: General. 1991;120:235–253. doi: 10.1037//0096-3445.120.3.235. [DOI] [PubMed] [Google Scholar]
- Conway CM, Christiansen MH. Sequential learning in non-human primates. Trends in Cognitive Sciences. 2001;5:539–546. doi: 10.1016/s1364-6613(00)01800-3. [DOI] [PubMed] [Google Scholar]
- Curran T. Effects of aging on implicit sequence learning: Accounting for sequence structure and explicit knowledge. Psychological Research. 1997a;60:24–41. doi: 10.1007/BF00419678. [DOI] [PubMed] [Google Scholar]
- Curran T. Higher-order associative learning in amnesia: Evidence from the serial reaction time task. Journal of Cognitive Neuroscience. 1997b;9:522–533. doi: 10.1162/jocn.1997.9.4.522. [DOI] [PubMed] [Google Scholar]
- Feeney JJ, Howard JH, Jr, Howard DV. Implicit learning of higher order sequences in middle age. Psychology and Aging. 2002;17:351–355. [PubMed] [Google Scholar]
- Folstein MF, Folstein SE, McHugh PR. “Mini-mental state”: A practical method for grading the cognitive state of patients for the clinician”. Journal of Psychiatric Research. 1975;12:189–198. doi: 10.1016/0022-3956(75)90026-6. [DOI] [PubMed] [Google Scholar]
- Frensch PA, Miner CS. Effects of presentation rate and individual differences in short-term memory capacity on an indirect measure of serial learning. Memory & Cognition. 1994;22:95–110. doi: 10.3758/bf03202765. [DOI] [PubMed] [Google Scholar]
- Gomez Beldarrain M, Grafman J, Ruiz De Velasco I, Pascual-Leone A, Garcia-Monco C. Prefrontal lesions impair the implicit and explicit learning of sequences on visuomotor tasks. Experimental Brain Research. 2002;142:578. doi: 10.1007/s00221-001-0935-2. [DOI] [PubMed] [Google Scholar]
- Howard DV, Howard JH., Jr Age differences in learning serial patterns: Direct versus indirect measures. Psychology and Aging. 1989;4:357–364. doi: 10.1037//0882-7974.4.3.357. [DOI] [PubMed] [Google Scholar]
- Howard DV, Howard JH., Jr Adult age differences in the rate of learning serial patterns: Evidence from direct and indirect tests. Psychology and Aging. 1992;7:232–241. doi: 10.1037//0882-7974.7.2.232. [DOI] [PubMed] [Google Scholar]
- Howard DV, Howard JH., Jr When it does hurt to try: Adult age differences in the effects of instructions on implicit pattern learning. Psychonomic Bulletin & Review. 2001;8:798–805. doi: 10.3758/bf03196220. [DOI] [PubMed] [Google Scholar]
- Howard JH, Jr, Howard DV. Age differences in implicit learning of higher order dependencies in serial patterns. Psychology and Aging. 1997;12:634–656. doi: 10.1037//0882-7974.12.4.634. [DOI] [PubMed] [Google Scholar]
- Hoyer, W. J., & Lincourt, A. E. (1998). Aging and the development of learning. In M. A. Stadler & P. A. Frensch (Eds.), Handbook of implicit learning. Thousand Oaks, CA: Sage.
- Japikse K, Howard DV, Howard JH., Jr Evaluation of a direct nonverbal measure of declarative sequence knowledge. Journal of Cognitive Neuroscience Supplement. 2001;12:62. [Google Scholar]
- Li SC. Connecting the many levels and facets of cognitive aging. Current Directions in Psychological Science. 2002;11:38–43. [Google Scholar]
- Light, L. L., Prull, M. W., LaVoie, D. J., & Healy, M. R. (2000). Dual-process theories of memory in old age. In T. J. Perfect & E. A. Maylor (Eds.), Models of cognitive aging (pp. 238–300). Oxford, England: Oxford University Press.
- Mitchell KJ, Johnson MK, Raye CL, Mather M, D’Esposito M. Aging and reflective processes of working memory: Binding and test load deficits. Psychology and Aging. 2000;15:527–541. doi: 10.1037//0882-7974.15.3.527. [DOI] [PubMed] [Google Scholar]
- Naveh-Benjamin M. Adult age differences in memory performance: Tests of an associative deficit hypothesis. Journal of Experimental Psychology: Learning, Memory and Cognition. 2000;26:1170–1187. doi: 10.1037//0278-7393.26.5.1170. [DOI] [PubMed] [Google Scholar]
- Negash S, Howard DV, Japikse KC, Howard JH., Jr Age-related differences in implicit learning of non-spatial sequences. Aging, Neuropsychology, and Cognition. 2003;10:108–121. [Google Scholar]
- Nissen MJ, Bullemer P. Attentional requirements of learning: Evidence from performance measures. Cognitive Psychology. 1987;19:1–32. [Google Scholar]
- Peigneux P, Maquet P, Meulemans T, Destrebecqz A, Laureys S, Degueldre C, et al. Striatum forever, despite sequence learning variability: A random effect analysis of PET data. Human Brain Mapping. 2000;10:179–194. doi: 10.1002/1097-0193(200008)10:4<179::AID-HBM30>3.0.CO;2-H. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prull, M. W., Gabrieli, J. D. E., & Bunge, S. A. (2000). Age-related changes in memory: A cognitive neuroscience perspective. In F. I. M. Craik & T. A. Salthouse (Eds.), The handbook of aging and cognition (2nd ed.). Mahwah, NJ: Erlbaum.
- Remillard G, Clark JM. Implicit learning of first-, second-, and third-order transition probabilities. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2001;27:483–498. doi: 10.1037/0278-7393.27.2.483. [DOI] [PubMed] [Google Scholar]
- Sakai K, Hikosaka O, Miyauchi S, Takino R, Sasaki Y, Putz B. Transition of brain activation from frontal to parietal areas in visuomotor sequence learning. Journal of Neuroscience. 1998;18:1827–1840. doi: 10.1523/JNEUROSCI.18-05-01827.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salthouse TA. The processing-speed theory of adult age differences in cognition. Psychological Review. 1996;103:403–428. doi: 10.1037/0033-295x.103.3.403. [DOI] [PubMed] [Google Scholar]
- Salthouse TA, McGuthry KE, Hambrick DZ. A framework for analyzing and interpreting differential aging patterns: Application to three measures of implicit learning. Aging, Neuropsychology, and Cognition. 1999;6:1–18. [Google Scholar]
- Schendan HE, Searl MM, Melrose RJ, Stern CE. An FMRI study of the role of the medial temporal lobe in implicit and explicit sequence learning. Neuron. 2003;37:1013–1025. doi: 10.1016/s0896-6273(03)00123-5. [DOI] [PubMed] [Google Scholar]
- Schvaneveldt RW, Gomez RL. Attention and probabilistic sequence learning. Psychological Research. 1998;61:175–190. [Google Scholar]
- Shanks DR, Channon S. Effects of a secondary task on “implicit” sequence learning: Learning or performance? Psychological Research. 2002;66:99–109. doi: 10.1007/s00426-001-0081-2. [DOI] [PubMed] [Google Scholar]
- Shanks DR, St. John MF. Characteristics of dissociable human learning systems. Behavioral and Brain Sciences. 1994;17:367–395. [Google Scholar]
- Wechsler, D. (1997a). Wechsler Adult Intelligence Scale (3rd ed.). San Antonio, TX: Psychological Corporation.
- Wechsler, D. (1997b). Wechsler Memory Scale (3rd ed.). San Antonio, TX: Psychological Corporation.
- Woodruff-Pak DS, Jaeger ME. Predictors of eyeblink classical conditioning over the adult age span. Psychology and Aging. 1998;13:193–205. doi: 10.1037//0882-7974.13.2.193. [DOI] [PubMed] [Google Scholar]


